Menu Close

dx-1-x-2-1-x-2-

Tinku Tara 0 Comments
Pin




Question Number 128775 by bramlexs22 last updated on 10/Jan/21
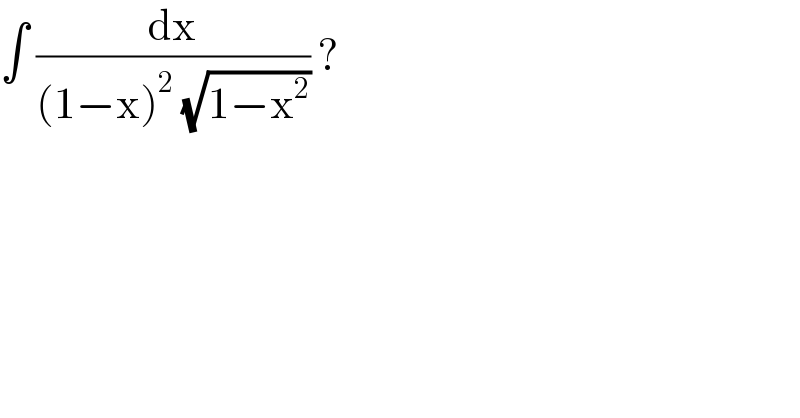
∫ (dx/((1−x)^2 (√(1−x^2 )))) ?
$$\int\:\frac{\mathrm{dx}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} \:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:? \\ $$
Answered by liberty last updated on 10/Jan/21
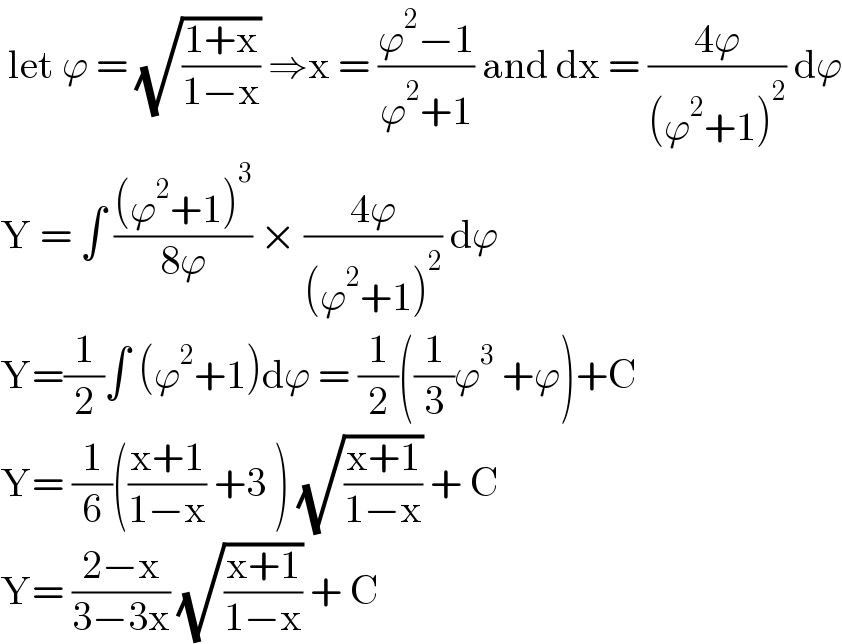
let ϕ = (√((1+x)/(1−x))) ⇒x = ((ϕ^2 −1)/(ϕ^2 +1)) and dx = ((4ϕ)/((ϕ^2 +1)^2 )) dϕ Y = ∫ (((ϕ^2 +1)^3 )/(8ϕ)) × ((4ϕ)/((ϕ^2 +1)^2 )) dϕ Y=(1/2)∫ (ϕ^2 +1)dϕ = (1/2)((1/3)ϕ^3 +ϕ)+C Y= (1/6)(((x+1)/(1−x)) +3 ) (√((x+1)/(1−x))) + C Y= ((2−x)/(3−3x)) (√((x+1)/(1−x))) + C
$$\:\mathrm{let}\:\varphi\:=\:\sqrt{\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}}\:\Rightarrow\mathrm{x}\:=\:\frac{\varphi^{\mathrm{2}} −\mathrm{1}}{\varphi^{\mathrm{2}} +\mathrm{1}}\:\mathrm{and}\:\mathrm{dx}\:=\:\frac{\mathrm{4}\varphi}{\left(\varphi^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{d}\varphi \\ $$$$\mathrm{Y}\:=\:\int\:\frac{\left(\varphi^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{8}\varphi}\:×\:\frac{\mathrm{4}\varphi}{\left(\varphi^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{d}\varphi \\ $$$$\mathrm{Y}=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\varphi^{\mathrm{2}} +\mathrm{1}\right)\mathrm{d}\varphi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}\varphi^{\mathrm{3}} \:+\varphi\right)+\mathrm{C} \\ $$$$\mathrm{Y}=\:\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:+\mathrm{3}\:\right)\:\sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{1}−\mathrm{x}}}\:+\:\mathrm{C} \\ $$$$\mathrm{Y}=\:\frac{\mathrm{2}−\mathrm{x}}{\mathrm{3}−\mathrm{3x}}\:\sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{1}−\mathrm{x}}}\:+\:\mathrm{C}\: \\ $$
Answered by mr W last updated on 10/Jan/21
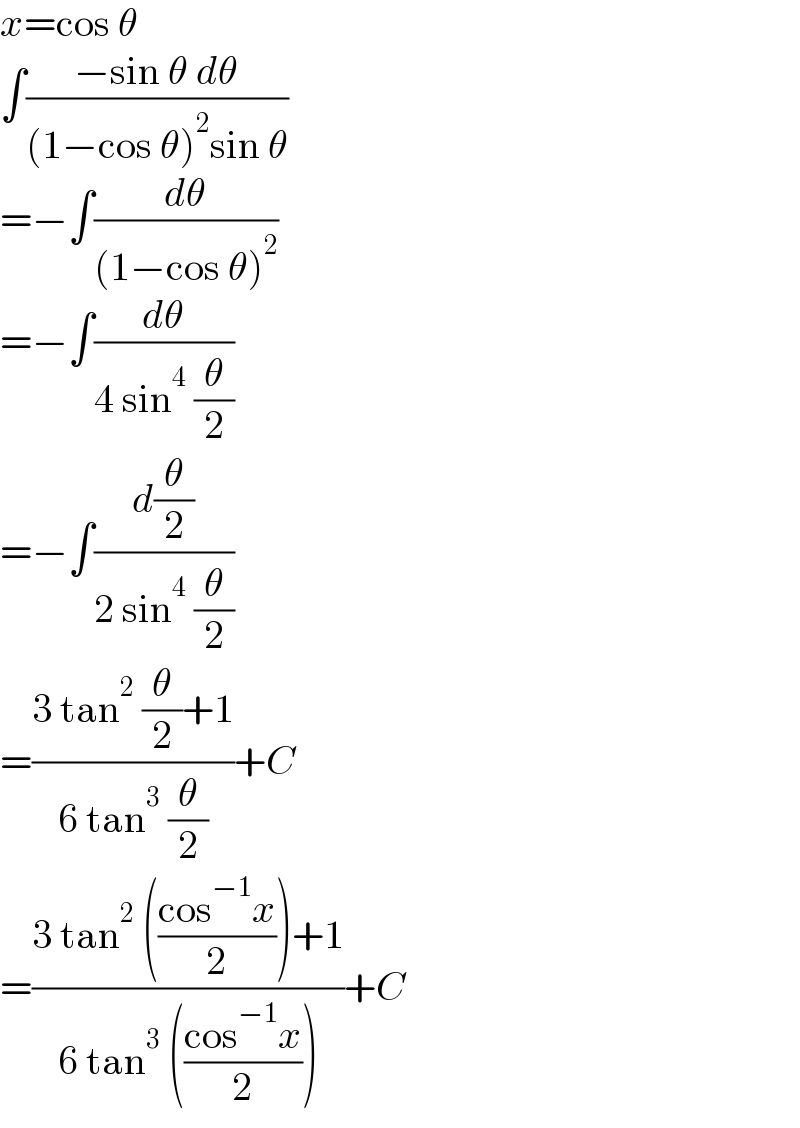
x=cos θ ∫((−sin θ dθ)/((1−cos θ)^2 sin θ)) =−∫(dθ/((1−cos θ)^2 )) =−∫(dθ/(4 sin^4 (θ/2))) =−∫(d(θ/2)/(2 sin^4 (θ/2))) =((3 tan^2 (θ/2)+1)/(6 tan^3 (θ/2)))+C =((3 tan^2 (((cos^(−1) x)/2))+1)/(6 tan^3 (((cos^(−1) x)/2))))+C
$${x}=\mathrm{cos}\:\theta \\ $$$$\int\frac{−\mathrm{sin}\:\theta\:{d}\theta}{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \mathrm{sin}\:\theta} \\ $$$$=−\int\frac{{d}\theta}{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} } \\ $$$$=−\int\frac{{d}\theta}{\mathrm{4}\:\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}} \\ $$$$=−\int\frac{{d}\frac{\theta}{\mathrm{2}}}{\mathrm{2}\:\mathrm{sin}^{\mathrm{4}} \:\frac{\theta}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{3}\:\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}+\mathrm{1}}{\mathrm{6}\:\mathrm{tan}^{\mathrm{3}} \:\frac{\theta}{\mathrm{2}}}+{C} \\ $$$$=\frac{\mathrm{3}\:\mathrm{tan}^{\mathrm{2}} \:\left(\frac{\mathrm{cos}^{−\mathrm{1}} {x}}{\mathrm{2}}\right)+\mathrm{1}}{\mathrm{6}\:\mathrm{tan}^{\mathrm{3}} \:\left(\frac{\mathrm{cos}^{−\mathrm{1}} {x}}{\mathrm{2}}\right)}+{C} \\ $$
Answered by mathmax by abdo last updated on 10/Jan/21
∫ (dx/((1−x)^2 (√(1−x^2 )))) changement x=sint give I =∫ ((cosx)/((1−sint)^2 cosx))dx =_(tan((t/2))=u) ∫ ((2du)/((1+u^2 )(1−((2u)/(1+u^2 )))^2 )) =∫ ((2du)/((u^2 +1)(((u^2 +1−2u)/(u^2 +1)))^2 )) =2∫ ((u^2 +1)/((u^2 −2u+1)^2 ))du =2 ∫ ((u^2 −2u+1 +2u)/((u^2 −2u+1)^2 ))du =2 ∫ (du/((u^2 −2u+1))) +2 ∫ ((2u−2 +2)/((u^2 −2u+1)^2 ))du =2∫ (du/((u−1)^2 )) +2 ∫ ((2u−2)/((u^2 −2u+1)^2 ))du+4∫ (du/((u−1)^4 )) =−(2/(u−1))−(2/(u^2 −2u+1)) +4 ×(1/(−4+1))(u−1)^(−4+1) +C =(2/(1−u))−(2/((1−u)^2 ))+(4/(3(1−u)^3 )) +C =(2/(1−tan((t/2))))−(2/((1−tan((t/2)))^2 )) +(4/(3(1−tan((t/2))))) +C =((10)/(3(1−tan(((arcsinx)/2)))))−(2/((1−tan(((arcsinx)/2)))^2 ))+C
$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{sint}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int\:\:\:\frac{\mathrm{cosx}}{\left(\mathrm{1}−\mathrm{sint}\right)^{\mathrm{2}} \mathrm{cosx}}\mathrm{dx}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}} \int\:\:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{\mathrm{2du}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)\left(\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}−\mathrm{2u}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\:=\mathrm{2}\int\:\:\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{2u}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du} \\ $$$$=\mathrm{2}\:\int\:\:\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{2u}+\mathrm{1}\:+\mathrm{2u}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{2u}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du}\:=\mathrm{2}\:\int\:\frac{\mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{2u}+\mathrm{1}\right)}\:+\mathrm{2}\:\int\:\frac{\mathrm{2u}−\mathrm{2}\:+\mathrm{2}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{2u}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du} \\ $$$$=\mathrm{2}\int\:\frac{\mathrm{du}}{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} }\:+\mathrm{2}\:\int\:\frac{\mathrm{2u}−\mathrm{2}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{2u}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du}+\mathrm{4}\int\:\:\frac{\mathrm{du}}{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=−\frac{\mathrm{2}}{\mathrm{u}−\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{u}^{\mathrm{2}} −\mathrm{2u}+\mathrm{1}}\:+\mathrm{4}\:×\frac{\mathrm{1}}{−\mathrm{4}+\mathrm{1}}\left(\mathrm{u}−\mathrm{1}\right)^{−\mathrm{4}+\mathrm{1}} \:+\mathrm{C} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{u}}−\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{3}} }\:+\mathrm{C} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}−\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }\:+\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{1}−\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\right)}\:+\mathrm{C} \\ $$$$=\frac{\mathrm{10}}{\mathrm{3}\left(\mathrm{1}−\mathrm{tan}\left(\frac{\mathrm{arcsinx}}{\mathrm{2}}\right)\right)}−\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{tan}\left(\frac{\mathrm{arcsinx}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *