Question Number 61719 by aliesam last updated on 06/Jun/19
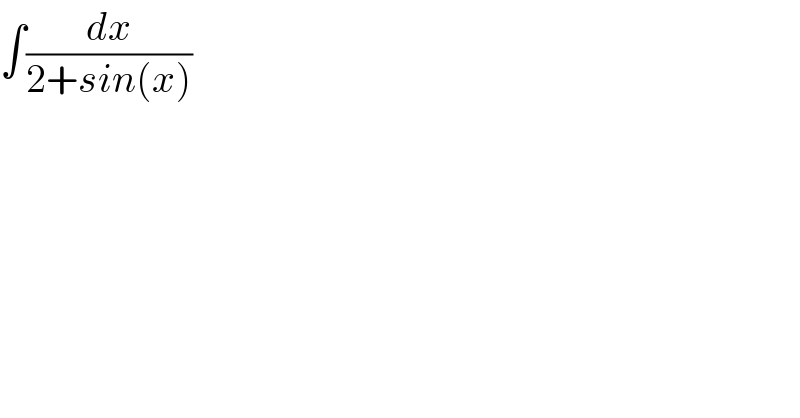
$$\int\frac{{dx}}{\mathrm{2}+{sin}\left({x}\right)} \\ $$
Commented by maxmathsup by imad last updated on 07/Jun/19
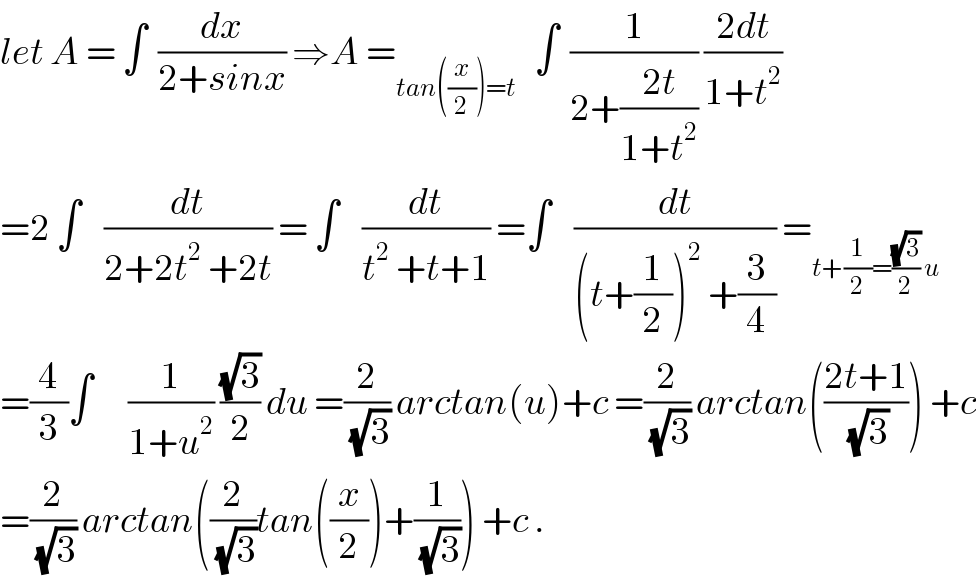
$${let}\:{A}\:=\:\int\:\:\frac{{dx}}{\mathrm{2}+{sinx}}\:\Rightarrow{A}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\int\:\:\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int\:\:\:\:\frac{{dt}}{\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}{t}}\:=\:\int\:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\:=\int\:\:\:\:\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{t}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{u}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{du}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left({u}\right)+{c}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+{c} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+{c}\:. \\ $$
