Question Number 125897 by john_santu last updated on 15/Dec/20
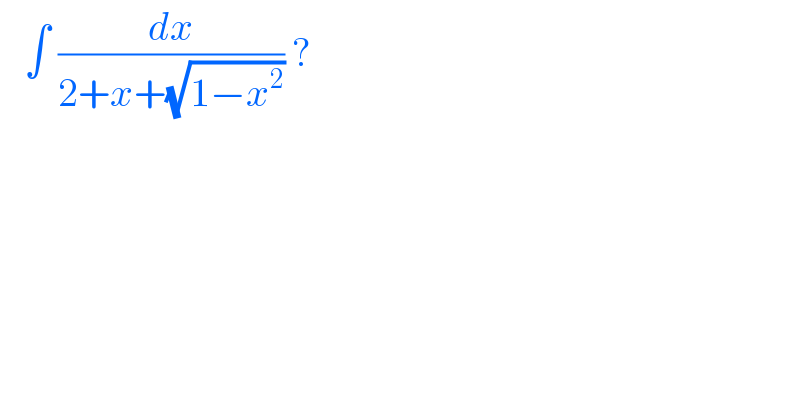
$$\:\:\:\int\:\frac{{dx}}{\mathrm{2}+{x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:?\: \\ $$
Commented by MJS_new last updated on 15/Dec/20
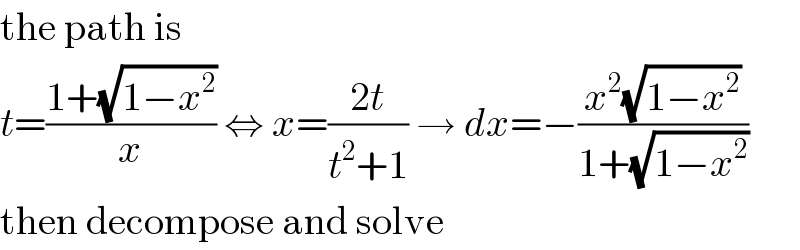
$$\mathrm{the}\:\mathrm{path}\:\mathrm{is} \\ $$$${t}=\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:\Leftrightarrow\:{x}=\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=−\frac{{x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{then}\:\mathrm{decompose}\:\mathrm{and}\:\mathrm{solve} \\ $$
Commented by liberty last updated on 15/Dec/20
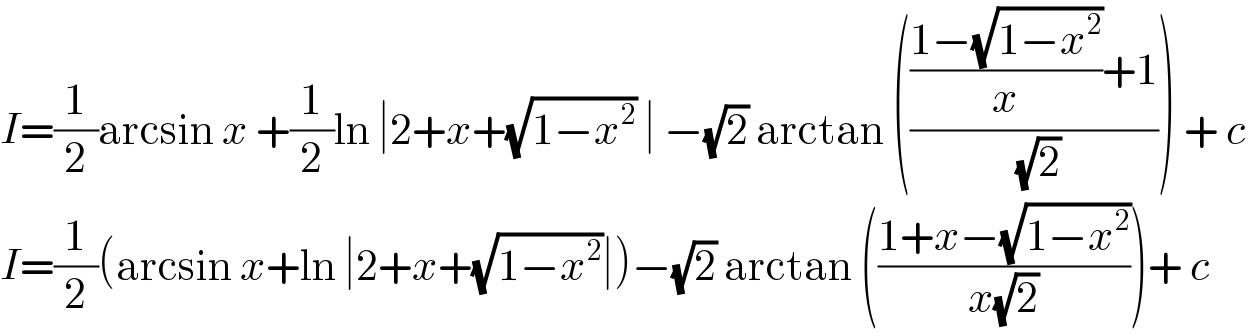
$${I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arcsin}\:{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{2}+{x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\mid\:−\sqrt{\mathrm{2}}\:\mathrm{arctan}\:\left(\frac{\frac{\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\:+\:{c}\: \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{arcsin}\:{x}+\mathrm{ln}\:\mid\mathrm{2}+{x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\mid\right)−\sqrt{\mathrm{2}}\:\mathrm{arctan}\:\left(\frac{\mathrm{1}+{x}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}\sqrt{\mathrm{2}}}\right)+\:{c} \\ $$
