Question Number 20244 by tammi last updated on 24/Aug/17

$$\int\frac{{dx}}{\left(\mathrm{2}−{x}\right)\sqrt{{x}}} \\ $$
Answered by ajfour last updated on 24/Aug/17
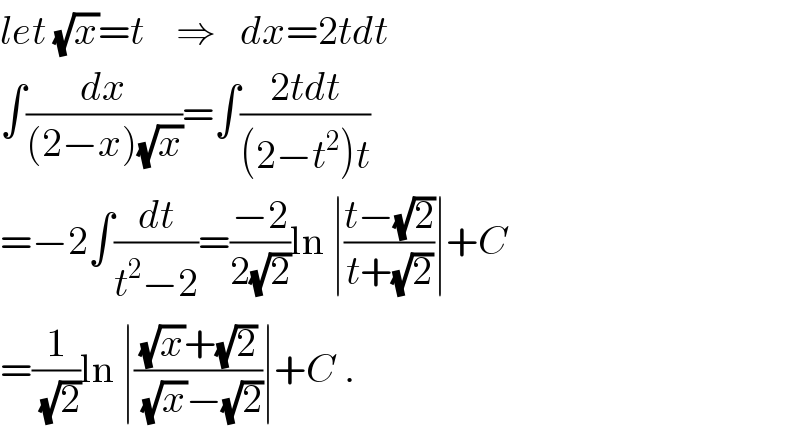
$${let}\:\sqrt{{x}}={t}\:\:\:\:\Rightarrow\:\:\:{dx}=\mathrm{2}{tdt} \\ $$$$\int\frac{{dx}}{\left(\mathrm{2}−{x}\right)\sqrt{{x}}}=\int\frac{\mathrm{2}{tdt}}{\left(\mathrm{2}−{t}^{\mathrm{2}} \right){t}} \\ $$$$=−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}}=\frac{−\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid\frac{{t}−\sqrt{\mathrm{2}}}{{t}+\sqrt{\mathrm{2}}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid\frac{\sqrt{{x}}+\sqrt{\mathrm{2}}}{\:\sqrt{{x}}−\sqrt{\mathrm{2}}}\mid+{C}\:. \\ $$
