Question Number 163638 by mkam last updated on 08/Jan/22
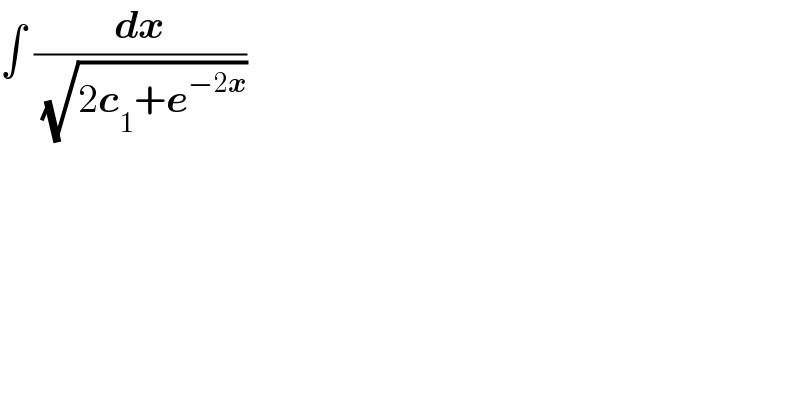
$$\int\:\frac{\boldsymbol{{dx}}}{\:\sqrt{\mathrm{2}\boldsymbol{{c}}_{\mathrm{1}} +\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{x}}} }} \\ $$
Commented by mkam last updated on 09/Jan/22

$$????? \\ $$
Commented by mr W last updated on 09/Jan/22
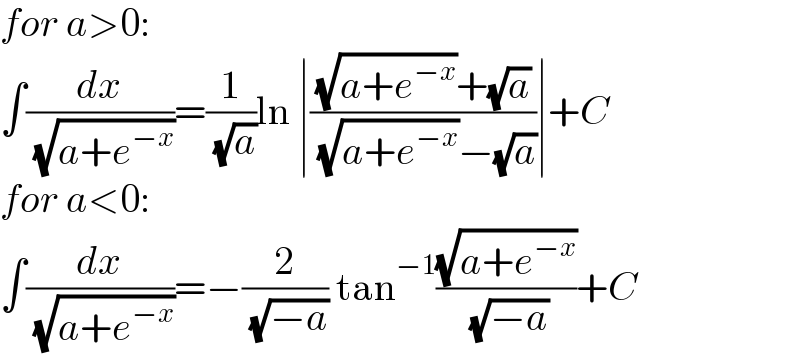
$${for}\:{a}>\mathrm{0}: \\ $$$$\int\frac{{dx}}{\:\sqrt{{a}+{e}^{−{x}} }}=\frac{\mathrm{1}}{\:\sqrt{{a}}}\mathrm{ln}\:\mid\frac{\sqrt{{a}+{e}^{−{x}} }+\sqrt{{a}}}{\:\sqrt{{a}+{e}^{−{x}} }−\sqrt{{a}}}\mid+{C} \\ $$$${for}\:{a}<\mathrm{0}: \\ $$$$\int\frac{{dx}}{\:\sqrt{{a}+{e}^{−{x}} }}=−\frac{\mathrm{2}}{\:\sqrt{−{a}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{{a}+{e}^{−{x}} }}{\:\sqrt{−{a}}}+{C} \\ $$
