Question Number 128752 by naka3546 last updated on 10/Jan/21
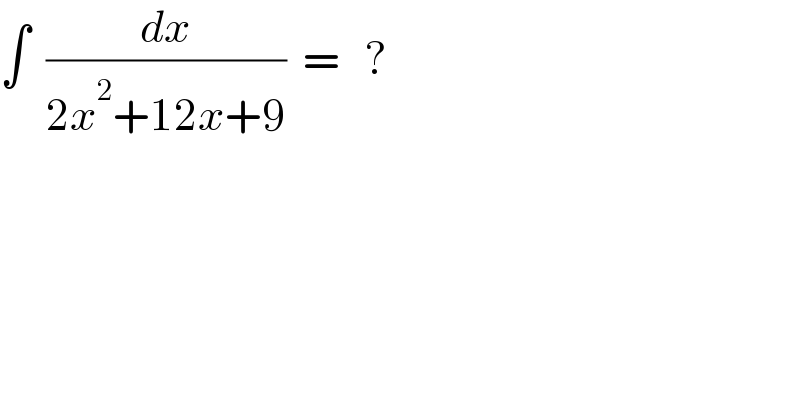
$$\int\:\:\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9}}\:\:=\:\:\:? \\ $$
Answered by mr W last updated on 10/Jan/21
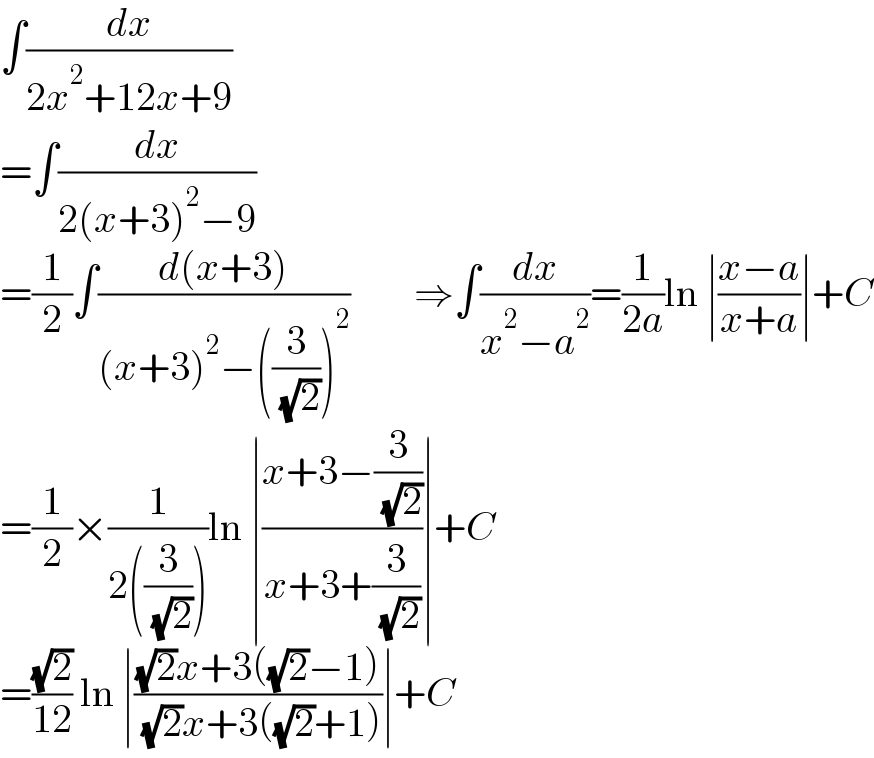
$$\int\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{9}} \\ $$$$=\int\frac{{dx}}{\mathrm{2}\left({x}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{9}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\mathrm{3}\right)}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }\:\:\:\:\:\:\:\:\Rightarrow\int\frac{{dx}}{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{a}}\mathrm{ln}\:\mid\frac{{x}−{a}}{{x}+{a}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right)}\mathrm{ln}\:\mid\frac{{x}+\mathrm{3}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}}{{x}+\mathrm{3}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}}\mid+{C} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{2}}{x}+\mathrm{3}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{2}}{x}+\mathrm{3}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}\mid+{C} \\ $$
Commented by naka3546 last updated on 10/Jan/21
$$\mathrm{thank}\:\mathrm{you}\:,\:{sir}\:. \\ $$
Answered by Dwaipayan Shikari last updated on 10/Jan/21
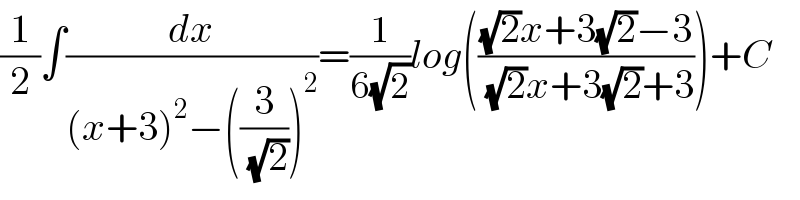
$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{2}}}{log}\left(\frac{\sqrt{\mathrm{2}}{x}+\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{3}}{\:\sqrt{\mathrm{2}}{x}+\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{3}}\right)+{C} \\ $$
Commented by naka3546 last updated on 10/Jan/21

$${thank}\:{you},\:{sir}. \\ $$
