Menu Close

dx-3sin-x-4cos-x-

Tinku Tara 0 Comments
Pin




Question Number 41561 by Tawa1 last updated on 09/Aug/18
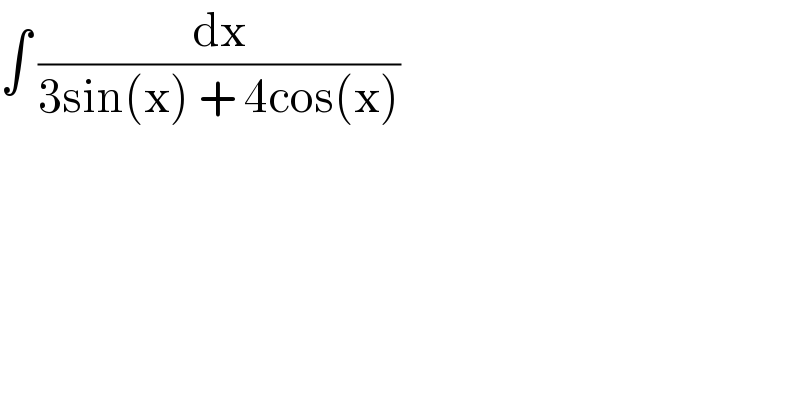
∫ (dx/(3sin(x) + 4cos(x)))
$$\int\:\frac{\mathrm{dx}}{\mathrm{3sin}\left(\mathrm{x}\right)\:+\:\mathrm{4cos}\left(\mathrm{x}\right)} \\ $$
Commented by math khazana by abdo last updated on 09/Aug/18
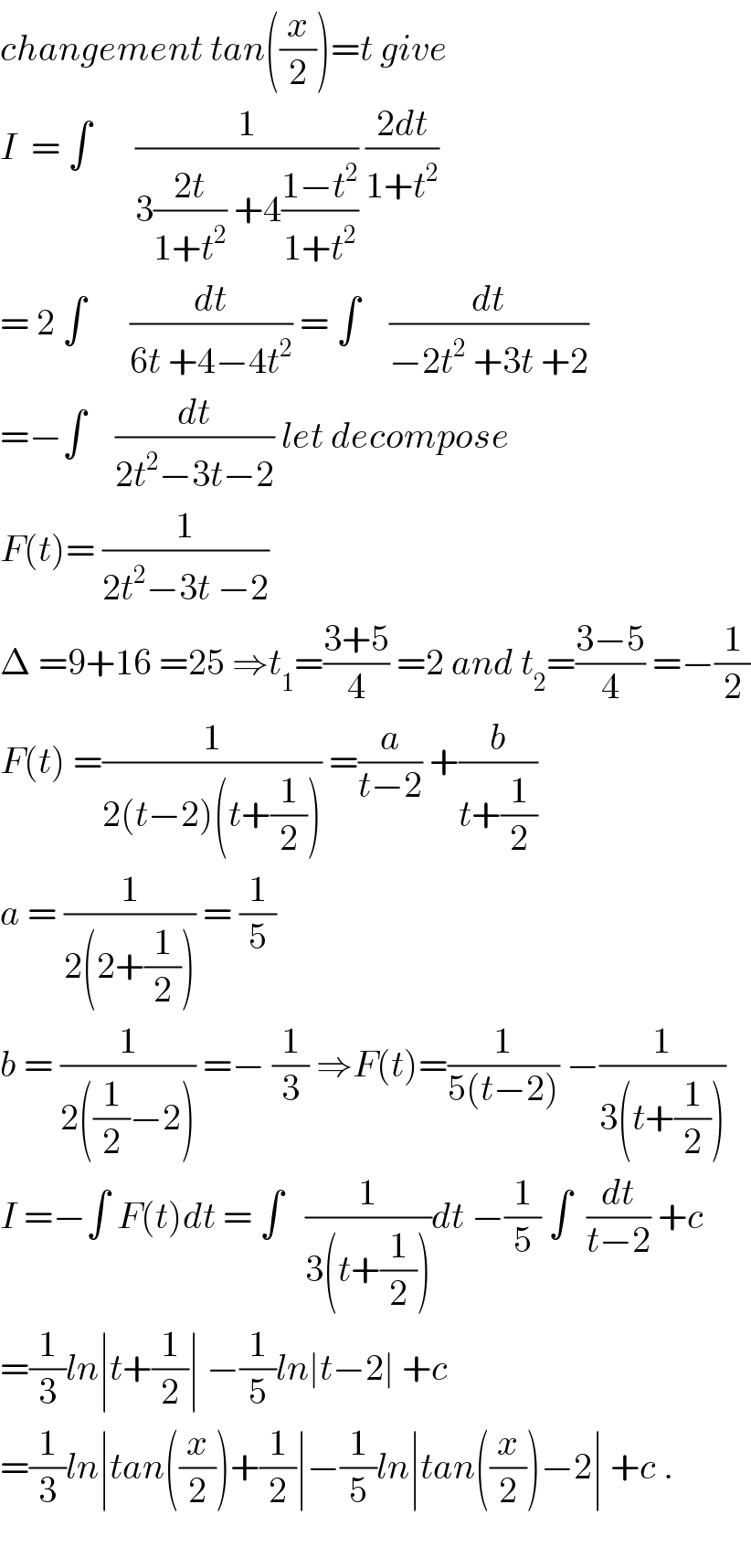
changement tan((x/2))=t give I = ∫ (1/(3((2t)/(1+t^2 )) +4((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = 2 ∫ (dt/(6t +4−4t^2 )) = ∫ (dt/(−2t^2 +3t +2)) =−∫ (dt/(2t^2 −3t−2)) let decompose F(t)= (1/(2t^2 −3t −2)) Δ =9+16 =25 ⇒t_1 =((3+5)/4) =2 and t_2 =((3−5)/4) =−(1/2) F(t) =(1/(2(t−2)(t+(1/2)))) =(a/(t−2)) +(b/(t+(1/2))) a = (1/(2(2+(1/2)))) = (1/5) b = (1/(2((1/2)−2))) =− (1/3) ⇒F(t)=(1/(5(t−2))) −(1/(3(t+(1/2)))) I =−∫ F(t)dt = ∫ (1/(3(t+(1/2))))dt −(1/5) ∫ (dt/(t−2)) +c =(1/3)ln∣t+(1/2)∣ −(1/5)ln∣t−2∣ +c =(1/3)ln∣tan((x/2))+(1/2)∣−(1/5)ln∣tan((x/2))−2∣ +c .
$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:\:=\:\int\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{4}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\:\int\:\:\:\:\:\:\frac{{dt}}{\mathrm{6}{t}\:+\mathrm{4}−\mathrm{4}{t}^{\mathrm{2}} }\:=\:\int\:\:\:\:\frac{{dt}}{−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{3}{t}\:+\mathrm{2}} \\ $$$$=−\int\:\:\:\:\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{2}}\:{let}\:{decompose} \\ $$$${F}\left({t}\right)=\:\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}\:−\mathrm{2}} \\ $$$$\Delta\:=\mathrm{9}+\mathrm{16}\:=\mathrm{25}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{5}}{\mathrm{4}}\:=\mathrm{2}\:{and}\:{t}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{5}}{\mathrm{4}}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\left({t}−\mathrm{2}\right)\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\frac{{a}}{{t}−\mathrm{2}}\:+\frac{{b}}{{t}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${a}\:=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${b}\:=\:\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)}\:=−\:\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{5}\left({t}−\mathrm{2}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$${I}\:=−\int\:{F}\left({t}\right){dt}\:=\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{3}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{dt}\:−\frac{\mathrm{1}}{\mathrm{5}}\:\int\:\:\frac{{dt}}{{t}−\mathrm{2}}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{t}+\frac{\mathrm{1}}{\mathrm{2}}\mid\:−\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid{t}−\mathrm{2}\mid\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mid−\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{2}\mid\:+{c}\:. \\ $$$$ \\ $$
Commented by Tawa1 last updated on 10/Aug/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by math khazana by abdo last updated on 10/Aug/18
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Aug/18
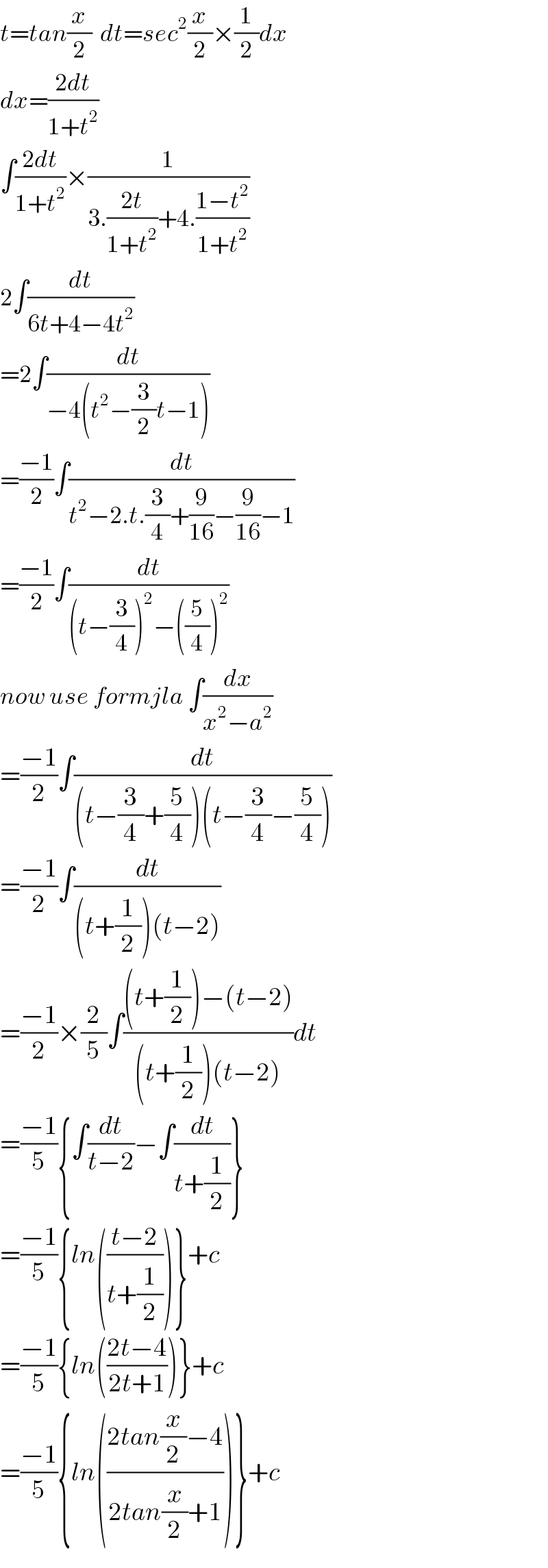
t=tan(x/2) dt=sec^2 (x/2)×(1/2)dx dx=((2dt)/(1+t^2 )) ∫((2dt)/(1+t^2 ))×(1/(3.((2t)/(1+t^2 ))+4.((1−t^2 )/(1+t^2 )))) 2∫(dt/(6t+4−4t^2 )) =2∫(dt/(−4(t^2 −(3/2)t−1))) =((−1)/2)∫(dt/(t^2 −2.t.(3/4)+(9/(16))−(9/(16))−1)) =((−1)/2)∫(dt/((t−(3/4))^2 −((5/4))^2 )) now use formjla ∫(dx/(x^2 −a^2 )) =((−1)/2)∫(dt/((t−(3/4)+(5/4))(t−(3/4)−(5/4)))) =((−1)/2)∫(dt/((t+(1/2))(t−2))) =((−1)/2)×(2/5)∫(((t+(1/2))−(t−2))/((t+(1/2))(t−2)))dt =((−1)/5){∫(dt/(t−2))−∫(dt/(t+(1/2)))} =((−1)/5){ln(((t−2)/(t+(1/2))))}+c =((−1)/5){ln(((2t−4)/(2t+1)))}+c =((−1)/5){ln(((2tan(x/2)−4)/(2tan(x/2)+1)))}+c
$${t}={tan}\frac{{x}}{\mathrm{2}}\:\:{dt}={sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}{dx} \\ $$$${dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{3}.\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{4}.\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\mathrm{2}\int\frac{{dt}}{\mathrm{6}{t}+\mathrm{4}−\mathrm{4}{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int\frac{{dt}}{−\mathrm{4}\left({t}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}{t}−\mathrm{1}\right)} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}.{t}.\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{9}}{\mathrm{16}}−\frac{\mathrm{9}}{\mathrm{16}}−\mathrm{1}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left({t}−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$${now}\:{use}\:{formjla}\:\int\frac{{dx}}{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left({t}−\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{4}}\right)\left({t}−\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{5}}{\mathrm{4}}\right)} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({t}−\mathrm{2}\right)} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{5}}\int\frac{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\left({t}−\mathrm{2}\right)}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({t}−\mathrm{2}\right)}{dt} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{5}}\left\{\int\frac{{dt}}{{t}−\mathrm{2}}−\int\frac{{dt}}{{t}+\frac{\mathrm{1}}{\mathrm{2}}}\right\} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{5}}\left\{{ln}\left(\frac{{t}−\mathrm{2}}{{t}+\frac{\mathrm{1}}{\mathrm{2}}}\right)\right\}+{c} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{5}}\left\{{ln}\left(\frac{\mathrm{2}{t}−\mathrm{4}}{\mathrm{2}{t}+\mathrm{1}}\right)\right\}+{c} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{5}}\left\{{ln}\left(\frac{\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}−\mathrm{4}}{\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}+\mathrm{1}}\right)\right\}+{c} \\ $$
Commented by Tawa1 last updated on 09/Aug/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 09/Aug/18
Umm. i would love it if you can finish it sir. God bless you sir. I am just learning
$$\mathrm{Umm}.\:\mathrm{i}\:\mathrm{would}\:\mathrm{love}\:\mathrm{it}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can}\:\mathrm{finish}\:\mathrm{it}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{just}\:\mathrm{learning} \\ $$
Commented by Tawa1 last updated on 09/Aug/18
I appreciate your effort sir. God bless you
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Aug/18
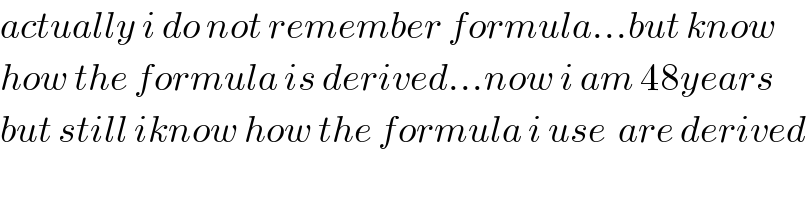
actually i do not remember formula...but know how the formula is derived...now i am 48years but still iknow how the formula i use are derived
$${actually}\:{i}\:{do}\:{not}\:{remember}\:{formula}…{but}\:{know} \\ $$$${how}\:{the}\:{formula}\:{is}\:{derived}…{now}\:{i}\:{am}\:\mathrm{48}{years} \\ $$$${but}\:{still}\:{iknow}\:{how}\:{the}\:{formula}\:{i}\:{use}\:\:{are}\:{derived} \\ $$
Commented by Tawa1 last updated on 09/Aug/18
Noted sir
$$\mathrm{Noted}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 09/Aug/18
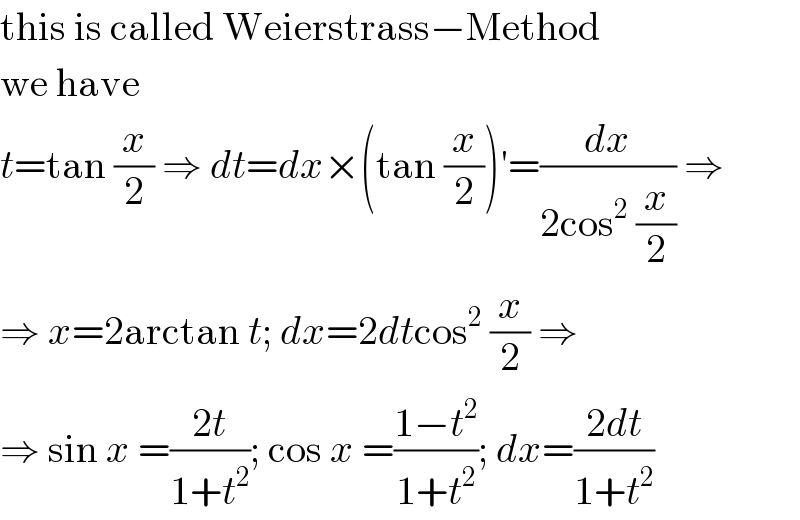
this is called Weierstrass−Method we have t=tan (x/2) ⇒ dt=dx×(tan (x/2))′=(dx/(2cos^2 (x/2))) ⇒ ⇒ x=2arctan t; dx=2dtcos^2 (x/2) ⇒ ⇒ sin x =((2t)/(1+t^2 )); cos x =((1−t^2 )/(1+t^2 )); dx=((2dt)/(1+t^2 ))
$$\mathrm{this}\:\mathrm{is}\:\mathrm{called}\:\mathrm{Weierstrass}−\mathrm{Method} \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Rightarrow\:{dt}={dx}×\left(\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right)'=\frac{{dx}}{\mathrm{2cos}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}}\:\Rightarrow \\ $$$$\Rightarrow\:{x}=\mathrm{2arctan}\:{t};\:{dx}=\mathrm{2}{dt}\mathrm{cos}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} };\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} };\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Aug/18
another method let 3=rcos∝ 4=rsin∝ ∫(dx/(rcos∝sinx+rsin∝cosx)) ∫(dx/(r{sin(x+∝)})) =(1/r)∫cosec(x+∝)dx now use formula and put value of r snd ∝ 3^2 +4^2 =r^2 (cos^2 ∝+sin^2 ∝) r^2 =25 so r=5 tan∝=(4/3) ∝=tan^(−1) ((4/3)) so ans is =(1/5)ln{tan(((x+α)/2))}+c =(1/5)ln{tan(((x+tan^(−1) ((4/3)))/2))}+c
$${another}\:{method} \\ $$$${let}\:\mathrm{3}={rcos}\propto\:\:\:\:\:\mathrm{4}={rsin}\propto \\ $$$$\int\frac{{dx}}{{rcos}\propto{sinx}+{rsin}\propto{cosx}} \\ $$$$\int\frac{{dx}}{{r}\left\{{sin}\left({x}+\propto\right)\right\}} \\ $$$$=\frac{\mathrm{1}}{{r}}\int{cosec}\left({x}+\propto\right){dx} \\ $$$${now}\:{use}\:{formula}\:{and}\:{put}\:{value}\:{of}\:{r}\:{snd}\:\propto \\ $$$$\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} ={r}^{\mathrm{2}} \left({cos}^{\mathrm{2}} \propto+{sin}^{\mathrm{2}} \propto\right) \\ $$$${r}^{\mathrm{2}} =\mathrm{25}\:\:{so}\:{r}=\mathrm{5} \\ $$$${tan}\propto=\frac{\mathrm{4}}{\mathrm{3}}\:\:\:\:\:\propto={tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$${so}\:{ans}\:{is}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}{ln}\left\{{tan}\left(\frac{{x}+\alpha}{\mathrm{2}}\right)\right\}+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}{ln}\left\{{tan}\left(\frac{{x}+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)}{\mathrm{2}}\right)\right\}+{c} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 09/Aug/18
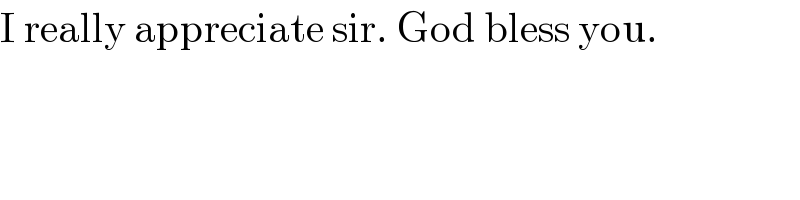
I really appreciate sir. God bless you.
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *