Menu Close

dx-3sin-x-sin-3-x-

Tinku Tara 0 Comments
Pin




Question Number 113275 by bemath last updated on 12/Sep/20
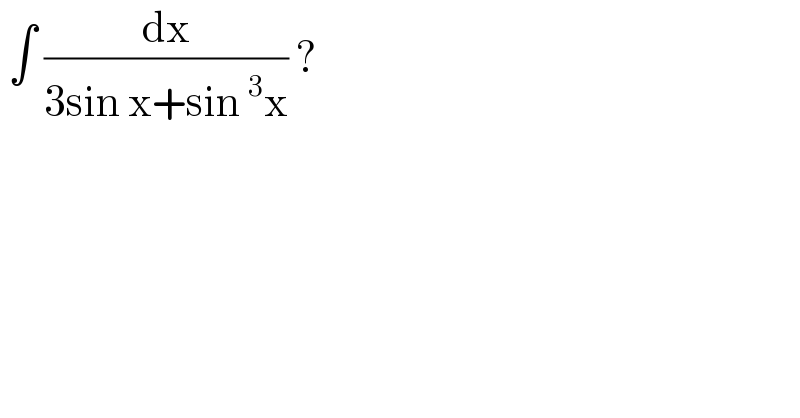
∫ (dx/(3sin x+sin^3 x)) ?
$$\:\int\:\frac{\mathrm{dx}}{\mathrm{3sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}\:? \\ $$
Answered by bemath last updated on 12/Sep/20
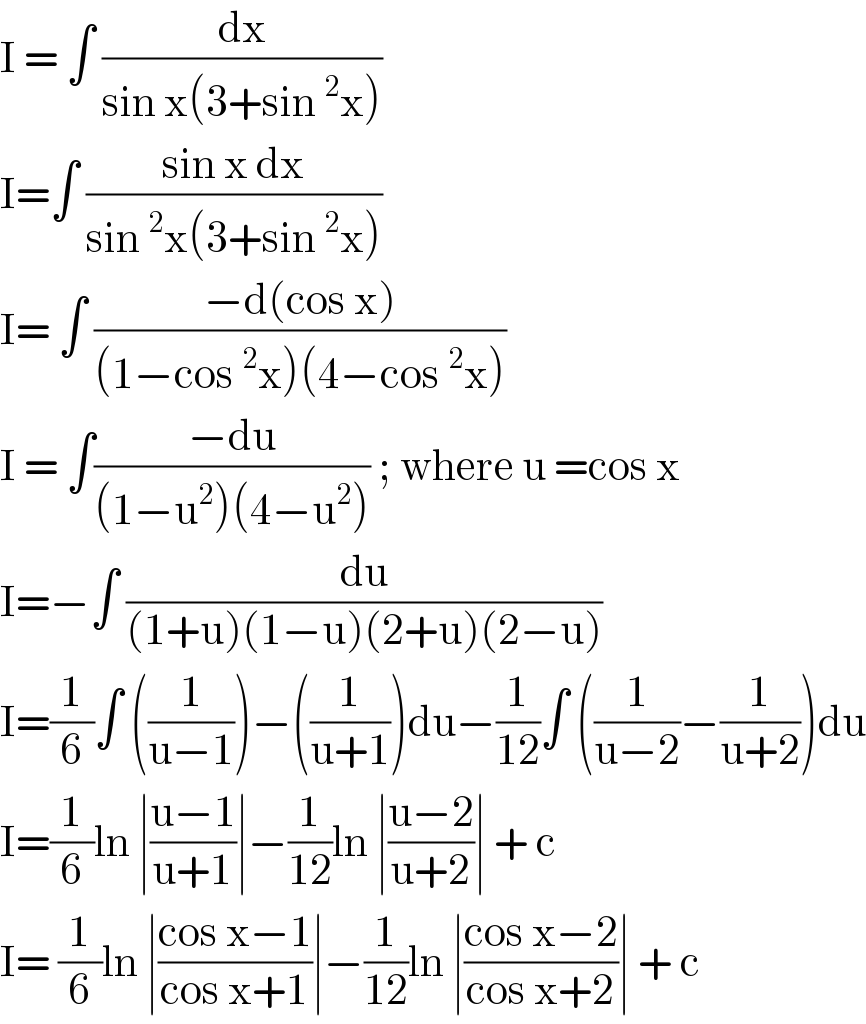
I = ∫ (dx/(sin x(3+sin^2 x))) I=∫ ((sin x dx)/(sin^2 x(3+sin^2 x))) I= ∫ ((−d(cos x))/((1−cos^2 x)(4−cos^2 x))) I = ∫((−du)/((1−u^2 )(4−u^2 ))) ; where u =cos x I=−∫ (du/((1+u)(1−u)(2+u)(2−u))) I=(1/6)∫ ((1/(u−1)))−((1/(u+1)))du−(1/(12))∫ ((1/(u−2))−(1/(u+2)))du I=(1/6)ln ∣((u−1)/(u+1))∣−(1/(12))ln ∣((u−2)/(u+2))∣ + c I= (1/6)ln ∣((cos x−1)/(cos x+1))∣−(1/(12))ln ∣((cos x−2)/(cos x+2))∣ + c
$$\mathrm{I}\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{sin}\:\mathrm{x}\left(\mathrm{3}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{3}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\mathrm{I}=\:\int\:\frac{−\mathrm{d}\left(\mathrm{cos}\:\mathrm{x}\right)}{\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{4}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\mathrm{I}\:=\:\int\frac{−\mathrm{du}}{\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{4}−\mathrm{u}^{\mathrm{2}} \right)}\:;\:\mathrm{where}\:\mathrm{u}\:=\mathrm{cos}\:\mathrm{x} \\ $$$$\mathrm{I}=−\int\:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}\right)\left(\mathrm{1}−\mathrm{u}\right)\left(\mathrm{2}+\mathrm{u}\right)\left(\mathrm{2}−\mathrm{u}\right)} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{6}}\int\:\left(\frac{\mathrm{1}}{\mathrm{u}−\mathrm{1}}\right)−\left(\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\right)\mathrm{du}−\frac{\mathrm{1}}{\mathrm{12}}\int\:\left(\frac{\mathrm{1}}{\mathrm{u}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{2}}\right)\mathrm{du} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\mid\frac{\mathrm{u}−\mathrm{1}}{\mathrm{u}+\mathrm{1}}\mid−\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\:\mid\frac{\mathrm{u}−\mathrm{2}}{\mathrm{u}+\mathrm{2}}\mid\:+\:\mathrm{c} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\mid\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{1}}{\mathrm{cos}\:\mathrm{x}+\mathrm{1}}\mid−\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\:\mid\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{2}}{\mathrm{cos}\:\mathrm{x}+\mathrm{2}}\mid\:+\:\mathrm{c} \\ $$
Answered by abdomsup last updated on 12/Sep/20
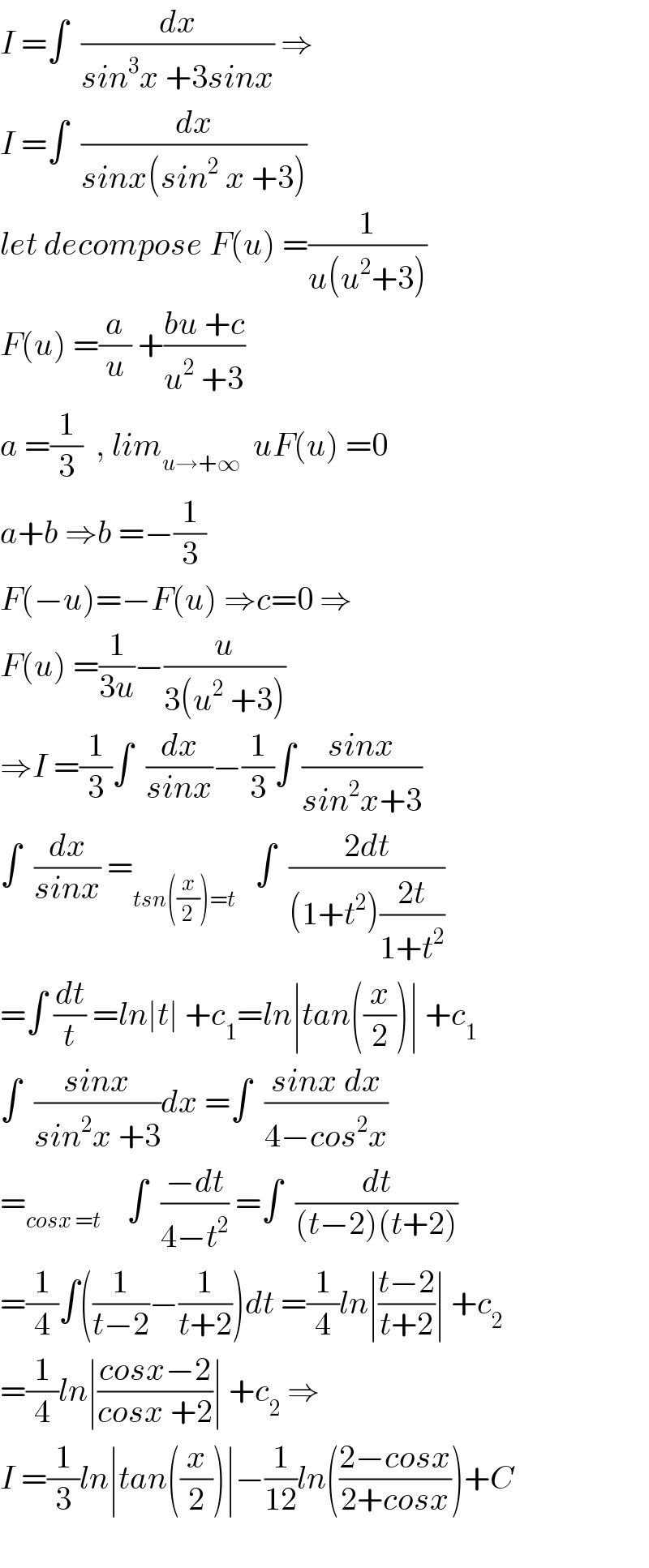
I =∫ (dx/(sin^3 x +3sinx)) ⇒ I =∫ (dx/(sinx(sin^2 x +3))) let decompose F(u) =(1/(u(u^2 +3))) F(u) =(a/u) +((bu +c)/(u^2 +3)) a =(1/3) , lim_(u→+∞) uF(u) =0 a+b ⇒b =−(1/3) F(−u)=−F(u) ⇒c=0 ⇒ F(u) =(1/(3u))−(u/(3(u^2 +3))) ⇒I =(1/3)∫ (dx/(sinx))−(1/3)∫ ((sinx)/(sin^2 x+3)) ∫ (dx/(sinx)) =_(tsn((x/2))=t) ∫ ((2dt)/((1+t^2 )((2t)/(1+t^2 )))) =∫ (dt/t) =ln∣t∣ +c_1 =ln∣tan((x/2))∣ +c_1 ∫ ((sinx)/(sin^2 x +3))dx =∫ ((sinx dx)/(4−cos^2 x)) =_(cosx =t) ∫ ((−dt)/(4−t^2 )) =∫ (dt/((t−2)(t+2))) =(1/4)∫((1/(t−2))−(1/(t+2)))dt =(1/4)ln∣((t−2)/(t+2))∣ +c_2 =(1/4)ln∣((cosx−2)/(cosx +2))∣ +c_2 ⇒ I =(1/3)ln∣tan((x/2))∣−(1/(12))ln(((2−cosx)/(2+cosx)))+C
$${I}\:=\int\:\:\frac{{dx}}{{sin}^{\mathrm{3}} {x}\:+\mathrm{3}{sinx}}\:\Rightarrow \\ $$$${I}\:=\int\:\:\frac{{dx}}{{sinx}\left({sin}^{\mathrm{2}} \:{x}\:+\mathrm{3}\right)} \\ $$$${let}\:{decompose}\:{F}\left({u}\right)\:=\frac{\mathrm{1}}{{u}\left({u}^{\mathrm{2}} +\mathrm{3}\right)} \\ $$$${F}\left({u}\right)\:=\frac{{a}}{{u}}\:+\frac{{bu}\:+{c}}{{u}^{\mathrm{2}} \:+\mathrm{3}} \\ $$$${a}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\:,\:{lim}_{{u}\rightarrow+\infty} \:\:{uF}\left({u}\right)\:=\mathrm{0} \\ $$$${a}+{b}\:\Rightarrow{b}\:=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${F}\left(−{u}\right)=−{F}\left({u}\right)\:\Rightarrow{c}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\frac{\mathrm{1}}{\mathrm{3}{u}}−\frac{{u}}{\mathrm{3}\left({u}^{\mathrm{2}} \:+\mathrm{3}\right)} \\ $$$$\Rightarrow{I}\:=\frac{\mathrm{1}}{\mathrm{3}}\int\:\:\frac{{dx}}{{sinx}}−\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{{sinx}}{{sin}^{\mathrm{2}} {x}+\mathrm{3}} \\ $$$$\int\:\:\frac{{dx}}{{sinx}}\:=_{{tsn}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\int\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$=\int\:\frac{{dt}}{{t}}\:={ln}\mid{t}\mid\:+{c}_{\mathrm{1}} ={ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid\:+{c}_{\mathrm{1}} \\ $$$$\int\:\:\frac{{sinx}}{{sin}^{\mathrm{2}} {x}\:+\mathrm{3}}{dx}\:=\int\:\:\frac{{sinx}\:{dx}}{\mathrm{4}−{cos}^{\mathrm{2}} {x}} \\ $$$$=_{{cosx}\:={t}} \:\:\:\:\int\:\:\frac{−{dt}}{\mathrm{4}−{t}^{\mathrm{2}} }\:=\int\:\:\frac{{dt}}{\left({t}−\mathrm{2}\right)\left({t}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left(\frac{\mathrm{1}}{{t}−\mathrm{2}}−\frac{\mathrm{1}}{{t}+\mathrm{2}}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{{t}−\mathrm{2}}{{t}+\mathrm{2}}\mid\:+{c}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{{cosx}−\mathrm{2}}{{cosx}\:+\mathrm{2}}\mid\:+{c}_{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid−\frac{\mathrm{1}}{\mathrm{12}}{ln}\left(\frac{\mathrm{2}−{cosx}}{\mathrm{2}+{cosx}}\right)+{C} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *