Question Number 102461 by bemath last updated on 09/Jul/20
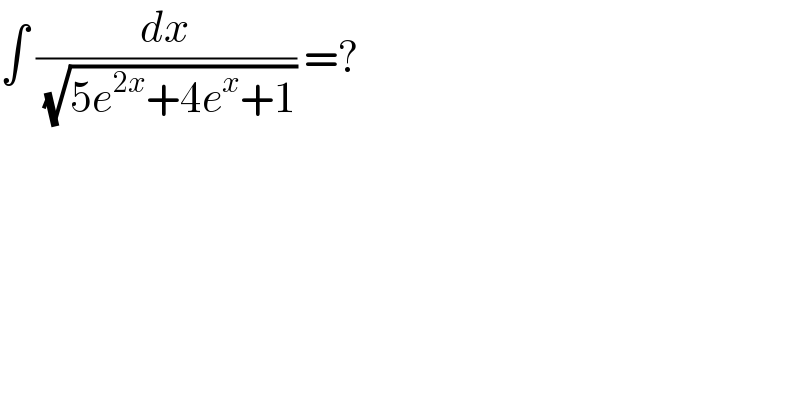
$$\int\:\frac{{dx}}{\:\sqrt{\mathrm{5}{e}^{\mathrm{2}{x}} +\mathrm{4}{e}^{{x}} +\mathrm{1}}}\:=? \\ $$
Answered by PRITHWISH SEN 2 last updated on 09/Jul/20
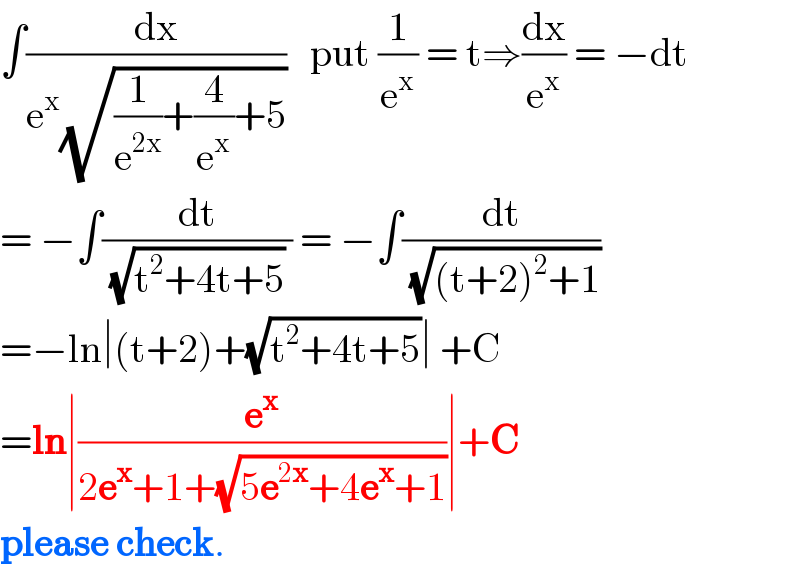
$$\int\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{x}} \sqrt{\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2x}} }+\frac{\mathrm{4}}{\mathrm{e}^{\mathrm{x}} }+\mathrm{5}}}\:\:\:\mathrm{put}\:\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{x}} }\:=\:\mathrm{t}\Rightarrow\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{x}} }\:=\:−\mathrm{dt} \\ $$$$=\:−\int\frac{\mathrm{dt}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{4t}+\mathrm{5}}\:}\:=\:−\int\frac{\mathrm{dt}}{\:\sqrt{\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}}} \\ $$$$=−\mathrm{ln}\mid\left(\mathrm{t}+\mathrm{2}\right)+\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{4t}+\mathrm{5}}\mid\:+\mathrm{C} \\ $$$$=\boldsymbol{\mathrm{ln}}\mid\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} }{\mathrm{2}\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\mathrm{1}+\sqrt{\mathrm{5}\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\mathrm{x}}} +\mathrm{4}\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} +\mathrm{1}}}\mid+\boldsymbol{\mathrm{C}} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
