Question Number 187530 by sciencestudentW last updated on 18/Feb/23
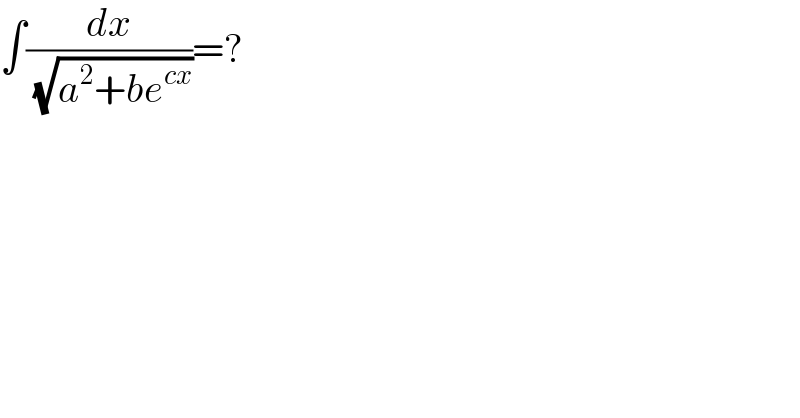
$$\int\frac{{dx}}{\:\sqrt{{a}^{\mathrm{2}} +{be}^{{cx}} }}=? \\ $$
Answered by anurup last updated on 18/Feb/23
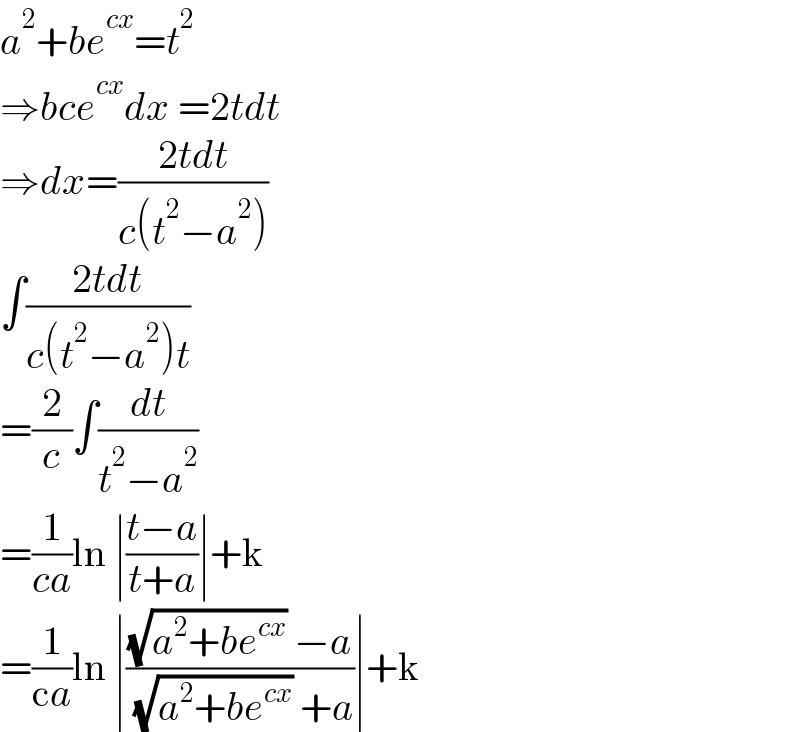
$${a}^{\mathrm{2}} +{be}^{{cx}} ={t}^{\mathrm{2}} \\ $$$$\Rightarrow{bce}^{{cx}} {dx}\:=\mathrm{2}{tdt} \\ $$$$\Rightarrow{dx}=\frac{\mathrm{2}{tdt}}{{c}\left({t}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)} \\ $$$$\int\frac{\mathrm{2}{tdt}}{{c}\left({t}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){t}} \\ $$$$=\frac{\mathrm{2}}{{c}}\int\frac{{dt}}{{t}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{{ca}}\mathrm{ln}\:\mid\frac{{t}−{a}}{{t}+{a}}\mid+\mathrm{k} \\ $$$$=\frac{\mathrm{1}}{\mathrm{c}{a}}\mathrm{ln}\:\mid\frac{\sqrt{{a}^{\mathrm{2}} +{be}^{{cx}} }\:−{a}}{\:\sqrt{{a}^{\mathrm{2}} +{be}^{{cx}} }\:+{a}}\mid+\mathrm{k} \\ $$
