Question Number 176648 by mokys last updated on 23/Sep/22
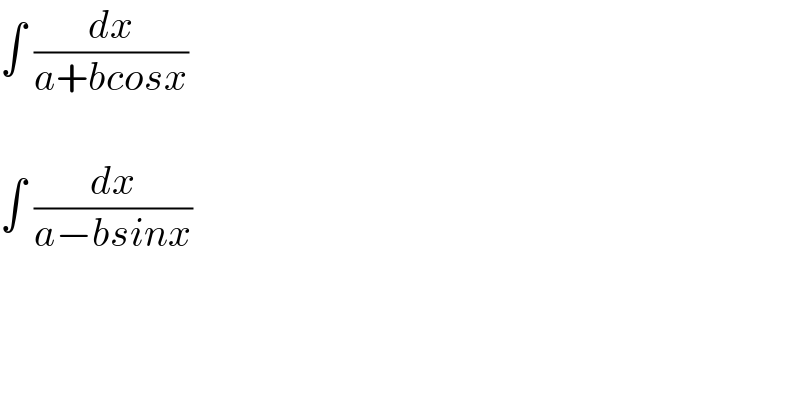
$$\int\:\frac{{dx}}{{a}+{bcosx}}\:\:\:\: \\ $$$$ \\ $$$$\int\:\frac{{dx}}{{a}−{bsinx}} \\ $$
Commented by mokys last updated on 24/Sep/22
![???]]]]](https://www.tinkutara.com/question/Q176655.png)
$$\left.?\left.?\left.?\left.\right]\right]\right]\right] \\ $$
Answered by Ar Brandon last updated on 24/Sep/22
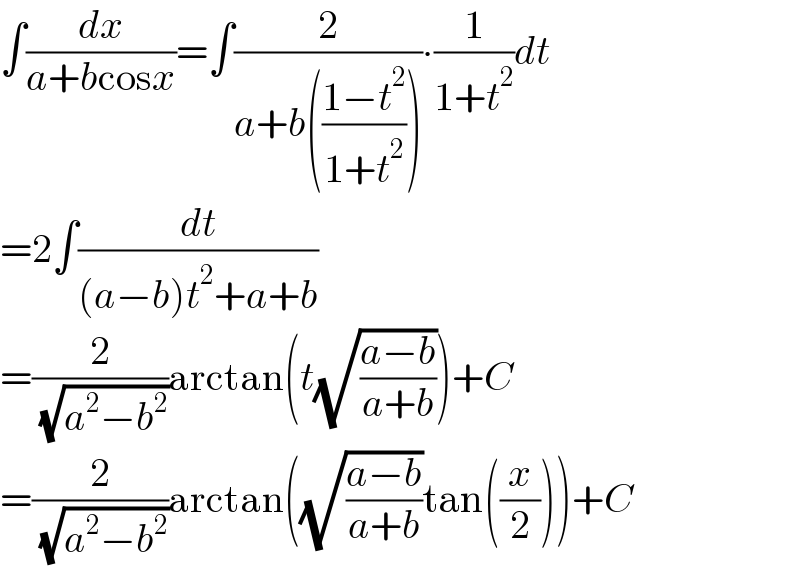
$$\int\frac{{dx}}{{a}+{b}\mathrm{cos}{x}}=\int\frac{\mathrm{2}}{{a}+{b}\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)}\centerdot\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{2}\int\frac{{dt}}{\left({a}−{b}\right){t}^{\mathrm{2}} +{a}+{b}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\mathrm{arctan}\left({t}\sqrt{\frac{{a}−{b}}{{a}+{b}}}\right)+{C} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\mathrm{arctan}\left(\sqrt{\frac{{a}−{b}}{{a}+{b}}}\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)+{C} \\ $$
Answered by BaliramKumar last updated on 24/Sep/22
![∫(( dx)/(a−bsinx)) = ∫(dx/(a−b[((2tan((x/2)))/(1+tan^2 ((x/2))))])) Let tan((x/2)) = y then sec^2 ((x/2))∙(1/2)∙dx = dy [1+tan^2 ((x/2))]∙(dx/2) = dy, dx = ((2dy)/(1+y^2 )) ∫(2/(a−b(((2y)/(1+y^2 )))))∙(dy/(1+y^2 )) = ∫((2dy)/(a+ay^2 −2by)) (2/a) ∫(dy/(y^2 −2((b/a))y+1)) = (2/a)∫(dy/((y−(b/a))^2 +(((√(a^2 −b^2 ))/a))^2 )) (2/a)∙(a/( (√(a^2 −b^2 ))))∙tan^(−1) (((ay−b)/( (√(a^2 −b^2 ))))) + C (2/( (√(a^2 −b^2 ))))∙tan^(−1) [((a∙tan((x/2))−b)/( (√(a^2 −b^2 ))))] + C](https://www.tinkutara.com/question/Q176670.png)
$$\int\frac{\:{dx}}{{a}−{bsinx}}\:=\:\int\frac{{dx}}{{a}−{b}\left[\frac{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\right]} \\ $$$${Let}\:\:\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)\:=\:{y}\:\:{then}\:\:\:{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot{dx}\:=\:{dy} \\ $$$$\:\:\:\left[\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right]\centerdot\frac{{dx}}{\mathrm{2}}\:=\:{dy},\:\:\:{dx}\:=\:\frac{\mathrm{2}{dy}}{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{2}}{{a}−{b}\left(\frac{\mathrm{2}{y}}{\mathrm{1}+{y}^{\mathrm{2}} }\right)}\centerdot\frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} }\:=\:\int\frac{\mathrm{2}{dy}}{{a}+{ay}^{\mathrm{2}} −\mathrm{2}{by}} \\ $$$$\frac{\mathrm{2}}{{a}}\:\int\frac{{dy}}{{y}^{\mathrm{2}} −\mathrm{2}\left(\frac{{b}}{{a}}\right){y}+\mathrm{1}}\:=\:\frac{\mathrm{2}}{{a}}\int\frac{{dy}}{\left({y}−\frac{{b}}{{a}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}{{a}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{{a}}\centerdot\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\centerdot{tan}^{−\mathrm{1}} \left(\frac{{ay}−{b}}{\:\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\right)\:+\:{C} \\ $$$$\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\centerdot{tan}^{−\mathrm{1}} \left[\frac{{a}\centerdot{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{b}}{\:\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\right]\:+\:{C} \\ $$
Commented by Tawa11 last updated on 25/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
