Question Number 104459 by bemath last updated on 21/Jul/20
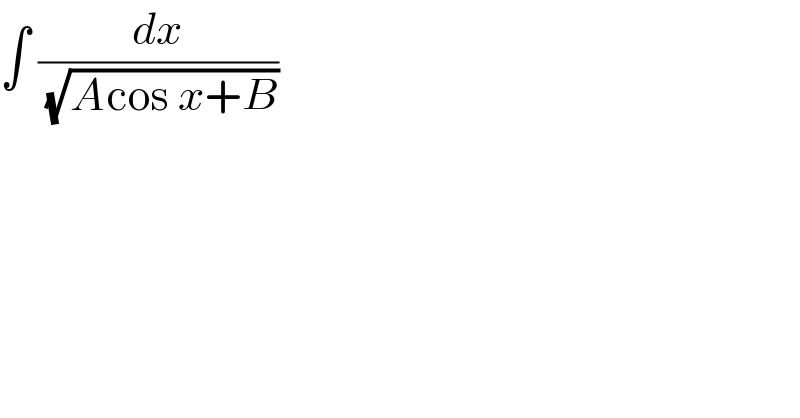
$$\int\:\frac{{dx}}{\:\sqrt{{A}\mathrm{cos}\:{x}+{B}}} \\ $$
Commented by Dwaipayan Shikari last updated on 21/Jul/20
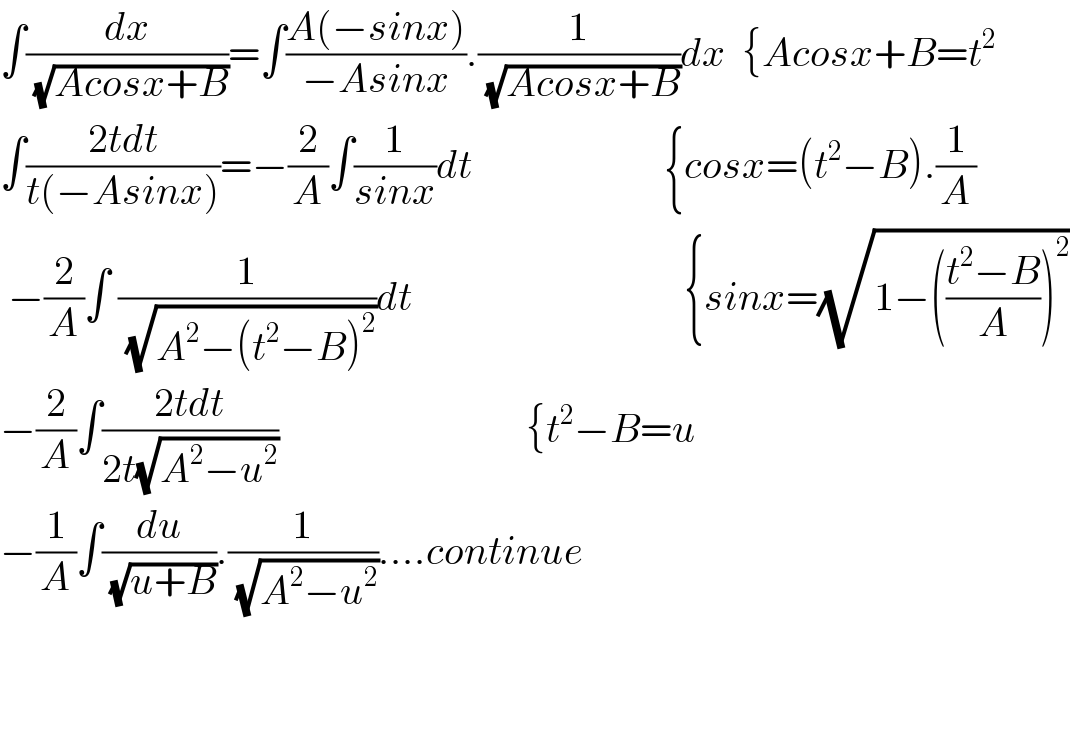
$$\int\frac{{dx}}{\:\sqrt{{Acosx}+{B}}}=\int\frac{{A}\left(−{sinx}\right)}{−{Asinx}}.\frac{\mathrm{1}}{\:\sqrt{{Acosx}+{B}}}{dx}\:\:\left\{{Acosx}+{B}={t}^{\mathrm{2}} \right. \\ $$$$\int\frac{\mathrm{2}{tdt}}{{t}\left(−{Asinx}\right)}=−\frac{\mathrm{2}}{{A}}\int\frac{\mathrm{1}}{{sinx}}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{cosx}=\left({t}^{\mathrm{2}} −{B}\right).\frac{\mathrm{1}}{{A}}\right. \\ $$$$\:−\frac{\mathrm{2}}{{A}}\int\:\frac{\mathrm{1}}{\:\sqrt{{A}^{\mathrm{2}} −\left({t}^{\mathrm{2}} −{B}\right)^{\mathrm{2}} }}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{sinx}=\sqrt{\mathrm{1}−\left(\frac{{t}^{\mathrm{2}} −{B}}{{A}}\right)^{\mathrm{2}} }\right. \\ $$$$−\frac{\mathrm{2}}{{A}}\int\frac{\mathrm{2}{tdt}}{\mathrm{2}{t}\sqrt{{A}^{\mathrm{2}} −{u}^{\mathrm{2}} }}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{t}^{\mathrm{2}} −{B}={u}\right. \\ $$$$−\frac{\mathrm{1}}{{A}}\int\frac{{du}}{\:\sqrt{{u}+{B}}}.\frac{\mathrm{1}}{\:\sqrt{{A}^{\mathrm{2}} −{u}^{\mathrm{2}} }}….{continue} \\ $$$$ \\ $$$$ \\ $$
Answered by bobhans last updated on 21/Jul/20
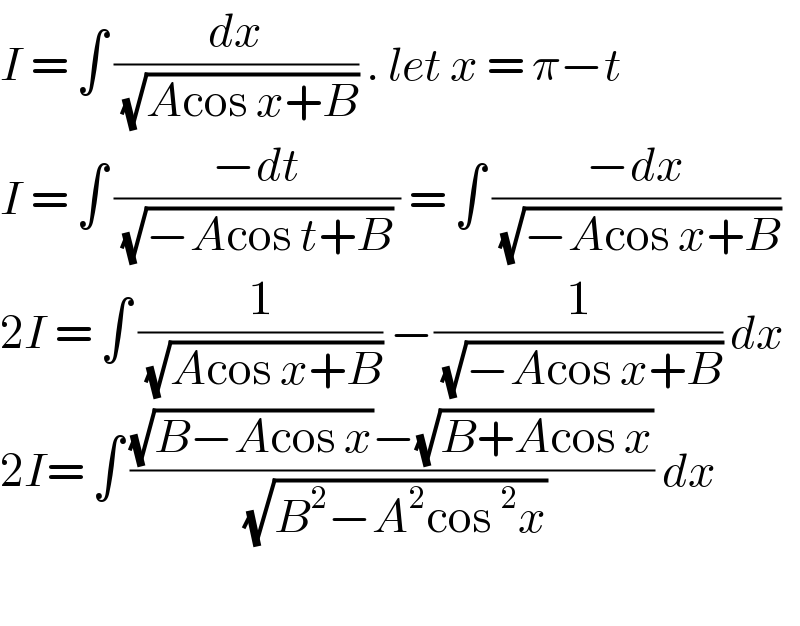
$${I}\:=\:\int\:\frac{{dx}}{\:\sqrt{{A}\mathrm{cos}\:{x}+{B}}}\:.\:{let}\:{x}\:=\:\pi−{t}\: \\ $$$${I}\:=\:\int\:\frac{−{dt}}{\:\sqrt{−{A}\mathrm{cos}\:{t}+{B}}\:}\:=\:\int\:\frac{−{dx}}{\:\sqrt{−{A}\mathrm{cos}\:{x}+{B}}} \\ $$$$\mathrm{2}{I}\:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{{A}\mathrm{cos}\:{x}+{B}}}\:−\frac{\mathrm{1}}{\:\sqrt{−{A}\mathrm{cos}\:{x}+{B}}}\:{dx} \\ $$$$\mathrm{2}{I}=\:\int\:\frac{\sqrt{{B}−{A}\mathrm{cos}\:{x}}−\sqrt{{B}+{A}\mathrm{cos}\:{x}}}{\:\sqrt{{B}^{\mathrm{2}} −{A}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {x}}}\:{dx} \\ $$$$ \\ $$
