Question Number 88064 by jagoll last updated on 08/Apr/20
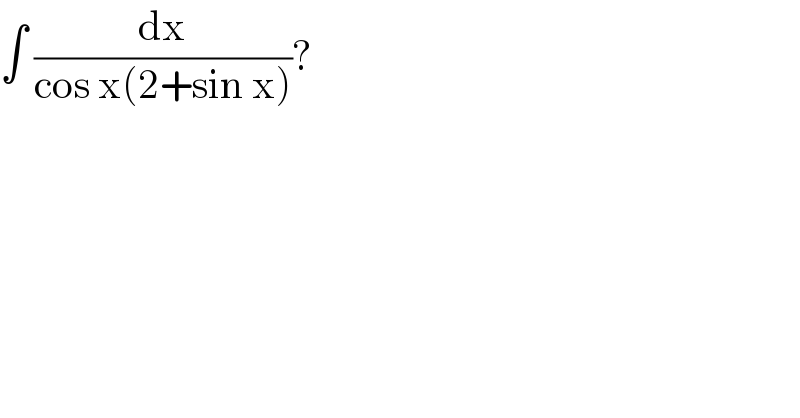
$$\int\:\frac{\mathrm{dx}}{\mathrm{cos}\:\mathrm{x}\left(\mathrm{2}+\mathrm{sin}\:\mathrm{x}\right)}? \\ $$
Answered by john santu last updated on 08/Apr/20
![∫ ((cos x dx)/(cos^2 x(2+sin x))) = ∫((d(sin x))/((1−sin^2 x)(2+sin x))) [ let 2+sin x = t ] ∫ (dt/(t(3−t)(t−1))) = ∫ (dt/(2(t−1)))+ ∫(dt/(6(3−t))) −∫(dt/(3t)) = (1/2)ln∣t−1∣−(1/6)ln∣3−t∣−(1/3)ln∣t∣ +c = (1/6)[3 ln∣1+sin x∣−ln∣1−sin x∣−2ln∣2+sin x∣] +c = (1/6)ln∣(((1+sin x)^3 )/((1−sin x)(2+sin x)^2 ))∣ + c](https://www.tinkutara.com/question/Q88066.png)
$$\int\:\frac{\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{2}+\mathrm{sin}\:\mathrm{x}\right)}\:=\:\int\frac{\mathrm{d}\left(\mathrm{sin}\:\mathrm{x}\right)}{\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{2}+\mathrm{sin}\:\mathrm{x}\right)} \\ $$$$\left[\:\mathrm{let}\:\mathrm{2}+\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{t}\:\right] \\ $$$$\int\:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{3}−\mathrm{t}\right)\left(\mathrm{t}−\mathrm{1}\right)}\:=\: \\ $$$$\int\:\frac{\mathrm{dt}}{\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}+\:\int\frac{\mathrm{dt}}{\mathrm{6}\left(\mathrm{3}−\mathrm{t}\right)}\:−\int\frac{\mathrm{dt}}{\mathrm{3t}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{t}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\mid\mathrm{3}−\mathrm{t}\mid−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{t}\mid\:+\mathrm{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{3}\:\mathrm{ln}\mid\mathrm{1}+\mathrm{sin}\:\mathrm{x}\mid−\mathrm{ln}\mid\mathrm{1}−\mathrm{sin}\:\mathrm{x}\mid−\mathrm{2ln}\mid\mathrm{2}+\mathrm{sin}\:\mathrm{x}\mid\right]\:+\mathrm{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\mid\frac{\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{3}} }{\left(\mathrm{1}−\mathrm{sin}\:\mathrm{x}\right)\left(\mathrm{2}+\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{2}} }\mid\:+\:\mathrm{c} \\ $$
