Menu Close

dx-cot-3-x-sin-7-x-

Tinku Tara 0 Comments
Pin




Question Number 178487 by cortano1 last updated on 17/Oct/22
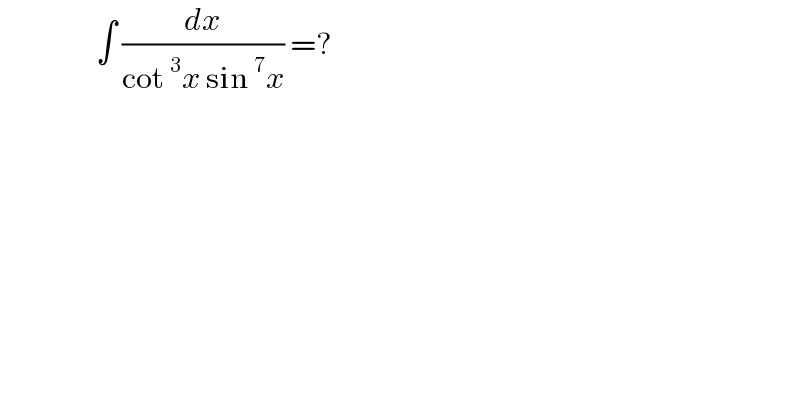
∫ (dx/(cot^3 x sin^7 x)) =?
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\:\frac{{dx}}{\mathrm{cot}\:^{\mathrm{3}} {x}\:\mathrm{sin}\:^{\mathrm{7}} {x}}\:=? \\ $$
Answered by Frix last updated on 18/Oct/22
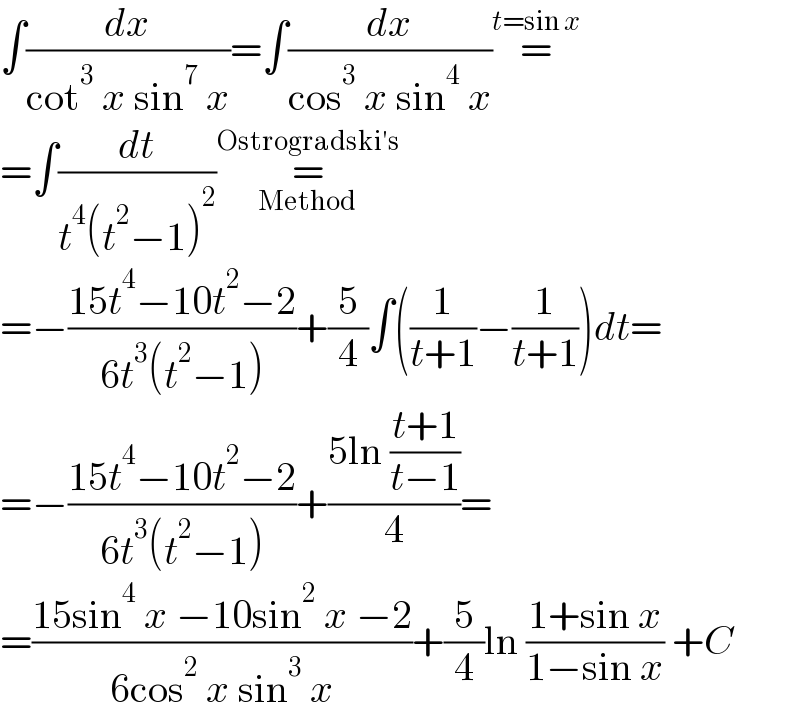
∫(dx/(cot^3 x sin^7 x))=∫(dx/(cos^3 x sin^4 x))=^(t=sin x) =∫(dt/(t^4 (t^2 −1)^2 ))=_(Method) ^(Ostrogradski′s) =−((15t^4 −10t^2 −2)/(6t^3 (t^2 −1)))+(5/4)∫((1/(t+1))−(1/(t+1)))dt= =−((15t^4 −10t^2 −2)/(6t^3 (t^2 −1)))+((5ln ((t+1)/(t−1)))/4)= =((15sin^4 x −10sin^2 x −2)/(6cos^2 x sin^3 x))+(5/4)ln ((1+sin x)/(1−sin x)) +C
$$\int\frac{{dx}}{\mathrm{cot}^{\mathrm{3}} \:{x}\:\mathrm{sin}^{\mathrm{7}} \:{x}}=\int\frac{{dx}}{\mathrm{cos}^{\mathrm{3}} \:{x}\:\mathrm{sin}^{\mathrm{4}} \:{x}}\overset{{t}=\mathrm{sin}\:{x}} {=} \\ $$$$=\int\frac{{dt}}{{t}^{\mathrm{4}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\underset{\mathrm{Method}} {\overset{\mathrm{Ostrogradski}'\mathrm{s}} {=}} \\ $$$$=−\frac{\mathrm{15}{t}^{\mathrm{4}} −\mathrm{10}{t}^{\mathrm{2}} −\mathrm{2}}{\mathrm{6}{t}^{\mathrm{3}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)}+\frac{\mathrm{5}}{\mathrm{4}}\int\left(\frac{\mathrm{1}}{{t}+\mathrm{1}}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}= \\ $$$$=−\frac{\mathrm{15}{t}^{\mathrm{4}} −\mathrm{10}{t}^{\mathrm{2}} −\mathrm{2}}{\mathrm{6}{t}^{\mathrm{3}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)}+\frac{\mathrm{5ln}\:\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}}{\mathrm{4}}= \\ $$$$=\frac{\mathrm{15sin}^{\mathrm{4}} \:{x}\:−\mathrm{10sin}^{\mathrm{2}} \:{x}\:−\mathrm{2}}{\mathrm{6cos}^{\mathrm{2}} \:{x}\:\mathrm{sin}^{\mathrm{3}} \:{x}}+\frac{\mathrm{5}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}\:+{C} \\ $$
Answered by Ar Brandon last updated on 17/Oct/22
I=∫(dx/(cot^3 xsin^7 x))=∫(dx/(cos^3 xsin^4 x))=∫((sec^7 x)/(tan^4 x))dx =−((sec^5 x)/(3tan^3 x))+(5/3)∫((sec^5 x)/(tan^2 x))dx=−((sec^5 x)/(3tan^3 x))−((5sec^3 x)/(3tanx))+5∫sec^3 xdx =−((sec^5 x)/(3tanx))−((5sec^3 x)/(3tanx))+5∫((cosx)/(cos^4 x))dx=−((sec^5 x)/(3tanx))−((5sec^3 x)/(3tanx))+5∫((cosx)/((1−sin^2 x)^2 ))dx =−((sec^5 x)/(3tanx))−((5sec^3 x)/(3tanx))+(5/4)∫((1/((1−sinx)^2 ))+(2/(1−sin^2 x))+(1/((1+sinx)^2 )))d(sinx) =−((sec^5 x)/(3tanx))−((5sec^3 x)/(3tanx))+(5/4)((1/(1−sinx))+2tanx−(1/(1+sinx)))+C =−((sec^5 x)/(3tanx))−((5sec^3 x)/(3tanx))+(5/2)secxtanx+(5/2)tanx+C
$${I}=\int\frac{{dx}}{\mathrm{cot}^{\mathrm{3}} {x}\mathrm{sin}^{\mathrm{7}} {x}}=\int\frac{{dx}}{\mathrm{cos}^{\mathrm{3}} {x}\mathrm{sin}^{\mathrm{4}} {x}}=\int\frac{\mathrm{sec}^{\mathrm{7}} {x}}{\mathrm{tan}^{\mathrm{4}} {x}}{dx} \\ $$$$\:\:=−\frac{\mathrm{sec}^{\mathrm{5}} {x}}{\mathrm{3tan}^{\mathrm{3}} {x}}+\frac{\mathrm{5}}{\mathrm{3}}\int\frac{\mathrm{sec}^{\mathrm{5}} {x}}{\mathrm{tan}^{\mathrm{2}} {x}}{dx}=−\frac{\mathrm{sec}^{\mathrm{5}} {x}}{\mathrm{3tan}^{\mathrm{3}} {x}}−\frac{\mathrm{5sec}^{\mathrm{3}} {x}}{\mathrm{3tan}{x}}+\mathrm{5}\int\mathrm{sec}^{\mathrm{3}} {xdx} \\ $$$$\:\:=−\frac{\mathrm{sec}^{\mathrm{5}} {x}}{\mathrm{3tan}{x}}−\frac{\mathrm{5sec}^{\mathrm{3}} {x}}{\mathrm{3tan}{x}}+\mathrm{5}\int\frac{\mathrm{cos}{x}}{\mathrm{cos}^{\mathrm{4}} {x}}{dx}=−\frac{\mathrm{sec}^{\mathrm{5}} {x}}{\mathrm{3tan}{x}}−\frac{\mathrm{5sec}^{\mathrm{3}} {x}}{\mathrm{3tan}{x}}+\mathrm{5}\int\frac{\mathrm{cos}{x}}{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx} \\ $$$$\:\:=−\frac{\mathrm{sec}^{\mathrm{5}} {x}}{\mathrm{3tan}{x}}−\frac{\mathrm{5sec}^{\mathrm{3}} {x}}{\mathrm{3tan}{x}}+\frac{\mathrm{5}}{\mathrm{4}}\int\left(\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{sin}{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}}+\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{sin}{x}\right)^{\mathrm{2}} }\right){d}\left(\mathrm{sin}{x}\right) \\ $$$$\:\:=−\frac{\mathrm{sec}^{\mathrm{5}} {x}}{\mathrm{3tan}{x}}−\frac{\mathrm{5sec}^{\mathrm{3}} {x}}{\mathrm{3tan}{x}}+\frac{\mathrm{5}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}{x}}+\mathrm{2tan}{x}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}{x}}\right)+{C} \\ $$$$\:\:=−\frac{\mathrm{sec}^{\mathrm{5}} {x}}{\mathrm{3tan}{x}}−\frac{\mathrm{5sec}^{\mathrm{3}} {x}}{\mathrm{3tan}{x}}+\frac{\mathrm{5}}{\mathrm{2}}\mathrm{sec}{x}\mathrm{tan}{x}+\frac{\mathrm{5}}{\mathrm{2}}\mathrm{tan}{x}+{C} \\ $$
Answered by greougoury555 last updated on 18/Oct/22
let s=sin x I= ∫ (ds/((1−s^2 )^2 s^4 )) =∫ (ds/(((1−s^2 )s^2 )^2 )) Partial fractions (1/([(1−s^2 )s^2 ]^2 )) = ((1/(1−s^2 )) +(1/s^2 ))^2 = ((1/(1−s^2 )))^2 +(2/((1−s^2 )s^2 )) +(1/s^4 ) = [ (1/2)((1/(1−s)) +(1/(1+s)))]^2 +(2/(1−s^2 )) +(2/s^2 )+(1/s^4 ) = (1/(4(1−s)^2 )) +(5/(2(1−s^2 )))+(1/(4(1+s)^2 ))+(2/s^2 )+(1/s^4 ) I=∫ (ds/((1−s^2 )^2 s^4 )) = ∫ [ (1/(4(1−s)^2 )) +(5/(2(1−s^2 )))+(1/(4(1+s)^2 ))+(2/s^2 )+(1/s^4 ) ]ds = (1/(4(1−s)))+(5/4) ln ∣((1+s)/(1−s)) ∣−(1/(4(1+s)))−(2/s)−(1/(3s^3 )) +c = (1/(4(1−sin x))) +(5/4) ln ∣((1+sin x)/(1−sin x))∣−(1/(4(1+sin x)))−(2/(sin x))−(1/(3sin^3 x)) + c
$$\:{let}\:{s}=\mathrm{sin}\:{x} \\ $$$$\:{I}=\:\int\:\frac{{ds}}{\left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{2}} {s}^{\mathrm{4}} }\:=\int\:\frac{{ds}}{\left(\left(\mathrm{1}−{s}^{\mathrm{2}} \right){s}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${Partial}\:{fractions}\: \\ $$$$\:\frac{\mathrm{1}}{\left[\left(\mathrm{1}−{s}^{\mathrm{2}} \right){s}^{\mathrm{2}} \:\right]^{\mathrm{2}} }\:=\:\left(\frac{\mathrm{1}}{\mathrm{1}−{s}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{s}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\:\:=\:\left(\frac{\mathrm{1}}{\mathrm{1}−{s}^{\mathrm{2}} }\right)^{\mathrm{2}} +\frac{\mathrm{2}}{\left(\mathrm{1}−{s}^{\mathrm{2}} \right){s}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{s}^{\mathrm{4}} } \\ $$$$\:=\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}−{s}}\:+\frac{\mathrm{1}}{\mathrm{1}+{s}}\right)\right]^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{1}−{s}^{\mathrm{2}} }\:+\frac{\mathrm{2}}{{s}^{\mathrm{2}} }+\frac{\mathrm{1}}{{s}^{\mathrm{4}} } \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}−{s}\right)^{\mathrm{2}} }\:+\frac{\mathrm{5}}{\mathrm{2}\left(\mathrm{1}−{s}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{{s}^{\mathrm{2}} }+\frac{\mathrm{1}}{{s}^{\mathrm{4}} } \\ $$$$\:{I}=\int\:\frac{{ds}}{\left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{2}} {s}^{\mathrm{4}} }\:=\:\int\:\left[\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}−{s}\right)^{\mathrm{2}} }\:+\frac{\mathrm{5}}{\mathrm{2}\left(\mathrm{1}−{s}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{{s}^{\mathrm{2}} }+\frac{\mathrm{1}}{{s}^{\mathrm{4}} }\:\right]{ds} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}−{s}\right)}+\frac{\mathrm{5}}{\mathrm{4}}\:\mathrm{ln}\:\mid\frac{\mathrm{1}+{s}}{\mathrm{1}−{s}}\:\mid−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+{s}\right)}−\frac{\mathrm{2}}{{s}}−\frac{\mathrm{1}}{\mathrm{3}{s}^{\mathrm{3}} }\:+{c} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}−\mathrm{sin}\:{x}\right)}\:+\frac{\mathrm{5}}{\mathrm{4}}\:\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}\mid−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+\mathrm{sin}\:{x}\right)}−\frac{\mathrm{2}}{\mathrm{sin}\:{x}}−\frac{\mathrm{1}}{\mathrm{3sin}\:^{\mathrm{3}} {x}}\:+\:{c}\: \\ $$$$\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *