Menu Close

dx-csc-x-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 175602 by cortano1 last updated on 03/Sep/22
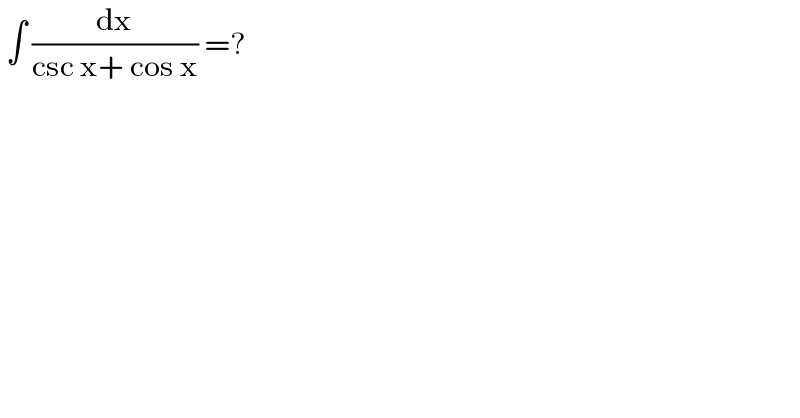
∫ (dx/(csc x+ cos x)) =?
$$\:\int\:\frac{\mathrm{dx}}{\mathrm{csc}\:\mathrm{x}+\:\mathrm{cos}\:\mathrm{x}}\:=? \\ $$
Commented by infinityaction last updated on 04/Sep/22
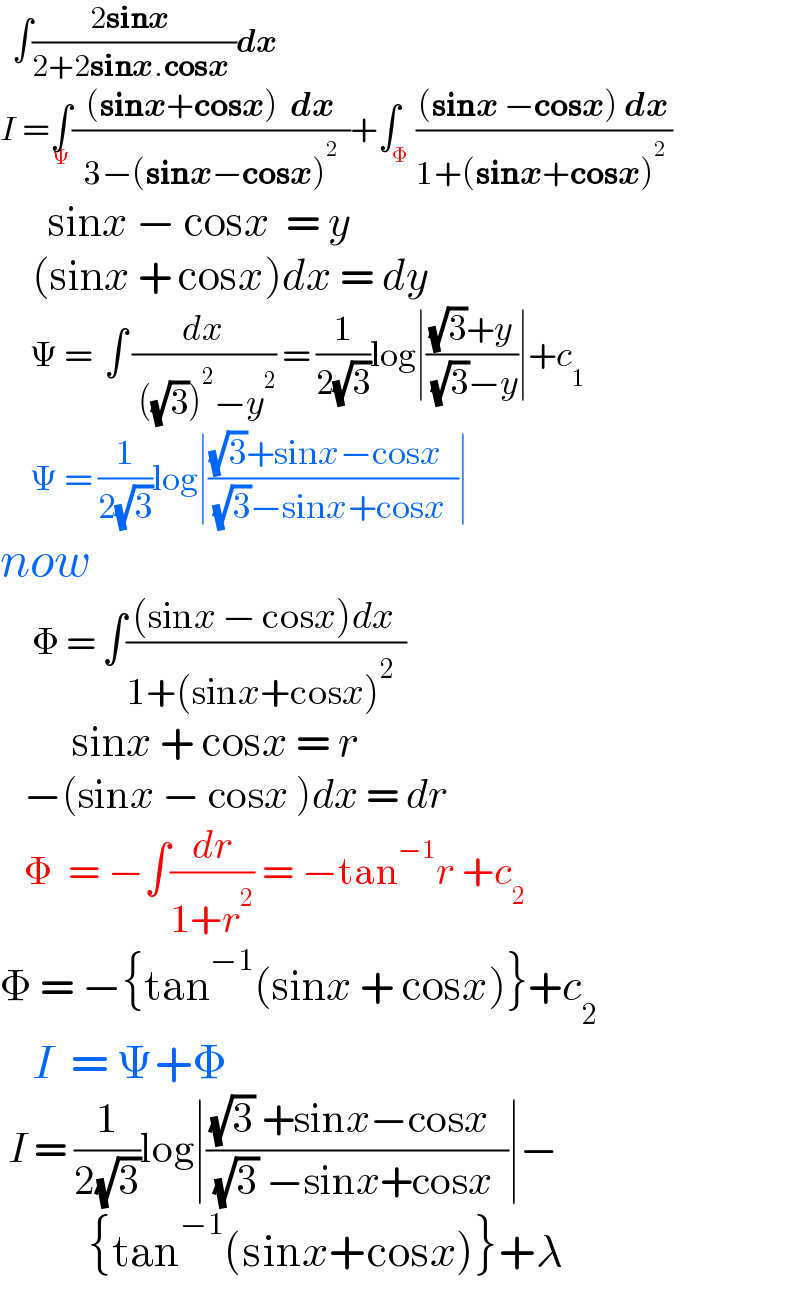
∫((2sinx )/(2+2sinx.cosx ))dx I =∫_Ψ (((sinx+cosx) dx)/( 3−(sinx−cosx)^2 ))+∫_Φ (((sinx −cosx) dx)/(1+(sinx+cosx)^2 )) sinx − cosx = y (sinx + cosx)dx = dy Ψ = ∫ (dx/( ((√3))^2 −y^2 )) = (1/(2(√3)))log∣(((√3)+y)/( (√3)−y))∣+c_1 Ψ = (1/(2(√3)))log∣(((√3)+sinx−cosx )/( (√3)−sinx+cosx ))∣ now Φ = ∫(((sinx − cosx)dx )/(1+(sinx+cosx)^2 )) sinx + cosx = r −(sinx − cosx )dx = dr Φ = −∫(dr/(1+r^2 )) = −tan^(−1) r +c_2 Φ = −{tan^(−1) (sinx + cosx)}+c_2 I = Ψ+Φ I = (1/(2(√3)))log∣(((√3) +sinx−cosx )/( (√3) −sinx+cosx ))∣− {tan^(−1) (sinx+cosx)}+λ
$$\:\:\int\frac{\mathrm{2}\boldsymbol{\mathrm{sin}{x}}\:}{\mathrm{2}+\mathrm{2}\boldsymbol{\mathrm{sin}{x}}.\boldsymbol{\mathrm{cos}{x}}\:}\boldsymbol{{dx}} \\ $$$${I}\:=\underset{\Psi} {\int}\frac{\left(\boldsymbol{\mathrm{sin}{x}}+\boldsymbol{\mathrm{cos}{x}}\right)\:\:\boldsymbol{{dx}}}{\:\:\mathrm{3}−\left(\boldsymbol{\mathrm{sin}{x}}−\boldsymbol{\mathrm{cos}{x}}\right)^{\mathrm{2}} \:\:}+\int_{\Phi} \frac{\left(\boldsymbol{\mathrm{sin}{x}}\:−\boldsymbol{\mathrm{cos}{x}}\right)\:\boldsymbol{{dx}}}{\mathrm{1}+\left(\boldsymbol{\mathrm{sin}{x}}+\boldsymbol{\mathrm{cos}{x}}\right)^{\mathrm{2}} \:} \\ $$$$\:\:\:\:\:\:\mathrm{sin}{x}\:−\:\mathrm{cos}{x}\:\:=\:{y} \\ $$$$\:\:\:\:\left(\mathrm{sin}{x}\:+\:\mathrm{cos}{x}\right){dx}\:=\:{dy} \\ $$$$\:\:\:\:\:\Psi\:=\:\:\int\:\frac{{dx}}{\:\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −{y}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{log}\mid\frac{\sqrt{\mathrm{3}}+{y}}{\:\sqrt{\mathrm{3}}−{y}}\mid+{c}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\Psi\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{log}\mid\frac{\sqrt{\mathrm{3}}+\mathrm{sin}{x}−\mathrm{cos}{x}\:\:}{\:\sqrt{\mathrm{3}}−\mathrm{sin}{x}+\mathrm{cos}{x}\:\:}\mid\: \\ $$$${now} \\ $$$$\:\:\:\:\Phi\:=\:\int\frac{\left(\mathrm{sin}{x}\:−\:\mathrm{cos}{x}\right){dx}\:}{\mathrm{1}+\left(\mathrm{sin}{x}+\mathrm{cos}{x}\right)^{\mathrm{2}} \:\:}\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{sin}{x}\:+\:\mathrm{cos}{x}\:=\:{r} \\ $$$$\:\:\:−\left(\mathrm{sin}{x}\:−\:\mathrm{cos}{x}\:\right){dx}\:=\:{dr} \\ $$$$\:\:\:\Phi\:\:=\:−\int\frac{{dr}}{\mathrm{1}+{r}^{\mathrm{2}} }\:=\:−\mathrm{tan}^{−\mathrm{1}} {r}\:+{c}_{\mathrm{2}} \:\: \\ $$$$\Phi\:=\:−\left\{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{sin}{x}\:+\:\mathrm{cos}{x}\right)\right\}+{c}_{\mathrm{2}} \: \\ $$$$\:\:\:\:{I}\:\:=\:\Psi+\Phi \\ $$$$\:{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{log}\mid\frac{\sqrt{\mathrm{3}}\:+\mathrm{sin}{x}−\mathrm{cos}{x}\:\:}{\:\sqrt{\mathrm{3}}\:−\mathrm{sin}{x}+\mathrm{cos}{x}\:\:}\mid− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left\{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{sin}{x}+\mathrm{cos}{x}\right)\right\}+\lambda\:\:\:\:\: \\ $$
Commented by Tawa11 last updated on 15/Sep/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Answered by Frix last updated on 03/Sep/22
∫(dx/(csc x +cos x))=_(dx=((2dt)/(t^2 +1))) ^(t=tan ((x/2)+(π/8))) =2(√2)∫((t^2 +2t−1)/(t^4 +10t^2 +1))dt= =((√3)/3)∫(((t−3+(√6))/(t^2 +5−2(√6)))−((t−3−(√6))/(t^2 +5+2(√6))))dt= =((√3)/6)ln (t^2 +5−2(√6)) −tan^(−1) (((√3)+(√2))t) − −((√3)/6)ln (t^2 +5+2(√6)) +tan^(−1) (((√3)−(√2))t) = =((√3)/6)ln ((t^2 +5−2(√6))/(t^2 +5+2(√6))) −tan^(−1) ((2(√2)t)/(t^2 +1)) the rest is easy
$$\int\frac{{dx}}{\mathrm{csc}\:{x}\:+\mathrm{cos}\:{x}}\underset{{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}} {\overset{{t}=\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)} {=}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\int\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{10}{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\int\left(\frac{{t}−\mathrm{3}+\sqrt{\mathrm{6}}}{{t}^{\mathrm{2}} +\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}−\frac{{t}−\mathrm{3}−\sqrt{\mathrm{6}}}{{t}^{\mathrm{2}} +\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}\right){dt}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)\:−\mathrm{tan}^{−\mathrm{1}} \:\left(\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right){t}\right)\:− \\ $$$$−\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)\:+\mathrm{tan}^{−\mathrm{1}} \:\left(\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right){t}\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}{{t}^{\mathrm{2}} +\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}\:−\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}{t}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *