Menu Close

dx-dy-y-xy-2-

Tinku Tara 0 Comments
Pin




Question Number 119933 by bramlexs22 last updated on 28/Oct/20
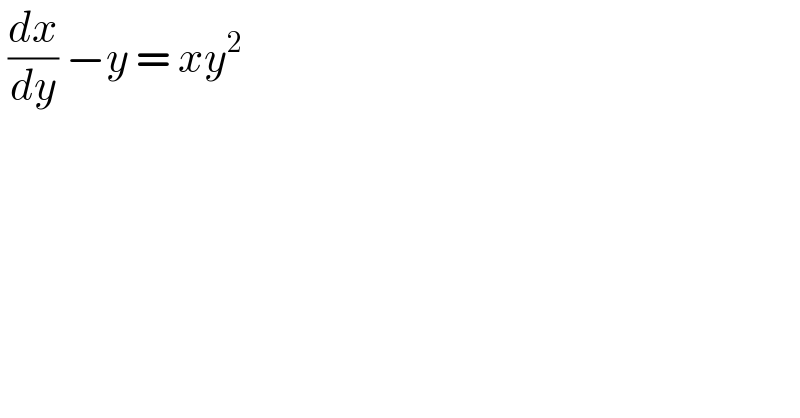
(dx/dy) −y = xy^2
$$\:\frac{{dx}}{{dy}}\:−{y}\:=\:{xy}^{\mathrm{2}} \\ $$
Answered by bobhans last updated on 28/Oct/20
(dy/dx) = (1/(y+xy^2 )) = ((1/y^2 )/((1/y)+x)) let (1/y)= u ⇒(du/dx) = −(1/y^2 ) (dy/dx) ⇔ (dy/dx) = −y^2 (du/dx) ⇔ −(1/u^2 ) (du/dx) = (u^2 /(u+x)) ; (du/dx) = ((−u^4 )/(u+x)) ...
$$\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}}{{y}+{xy}^{\mathrm{2}} }\:=\:\frac{\frac{\mathrm{1}}{{y}^{\mathrm{2}} }}{\frac{\mathrm{1}}{{y}}+{x}} \\ $$$${let}\:\frac{\mathrm{1}}{{y}}=\:{u}\:\Rightarrow\frac{{du}}{{dx}}\:=\:−\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\:\frac{{dy}}{{dx}} \\ $$$$\Leftrightarrow\:\frac{{dy}}{{dx}}\:=\:−{y}^{\mathrm{2}} \:\frac{{du}}{{dx}} \\ $$$$\Leftrightarrow\:−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\:\frac{{du}}{{dx}}\:=\:\frac{{u}^{\mathrm{2}} }{{u}+{x}}\:;\:\frac{{du}}{{dx}}\:=\:\frac{−{u}^{\mathrm{4}} }{{u}+{x}} \\ $$$$… \\ $$$$ \\ $$
Answered by Lordose last updated on 28/Oct/20
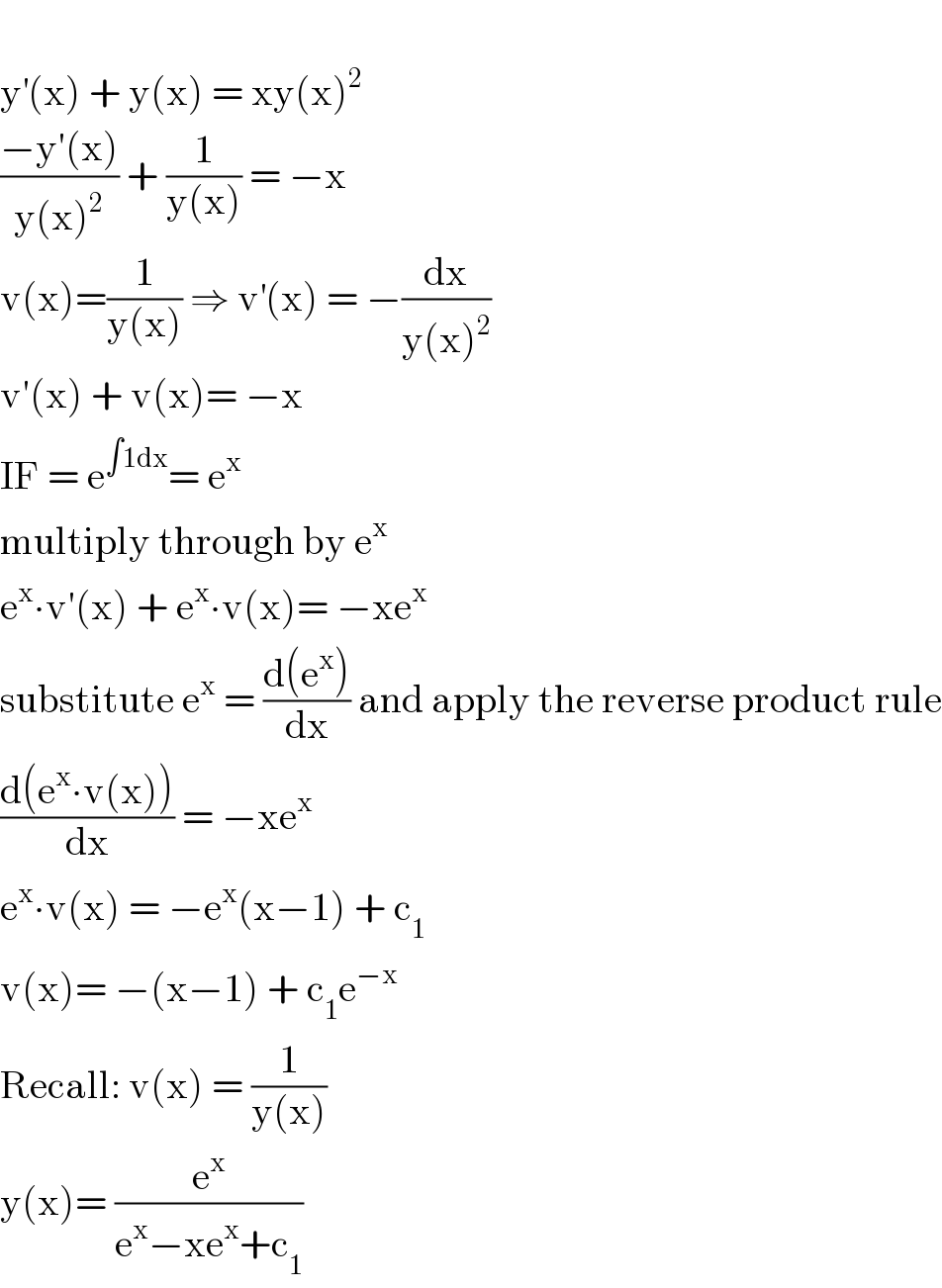
y^′ (x) + y(x) = xy(x)^2 ((−y′(x))/(y(x)^2 )) + (1/(y(x))) = −x v(x)=(1/(y(x))) ⇒ v^′ (x) = −(dx/(y(x)^2 )) v′(x) + v(x)= −x IF = e^(∫1dx) = e^x multiply through by e^x e^x ∙v′(x) + e^x ∙v(x)= −xe^x substitute e^x = ((d(e^x ))/dx) and apply the reverse product rule ((d(e^x ∙v(x)))/dx) = −xe^x e^x ∙v(x) = −e^x (x−1) + c_1 v(x)= −(x−1) + c_1 e^(−x) Recall: v(x) = (1/(y(x))) y(x)= (e^x /(e^x −xe^x +c_1 ))
$$ \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)\:+\:\mathrm{y}\left(\mathrm{x}\right)\:=\:\mathrm{xy}\left(\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\frac{−\mathrm{y}'\left(\mathrm{x}\right)}{\mathrm{y}\left(\mathrm{x}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{y}\left(\mathrm{x}\right)}\:=\:−\mathrm{x} \\ $$$$\mathrm{v}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{y}\left(\mathrm{x}\right)}\:\Rightarrow\:\mathrm{v}^{'} \left(\mathrm{x}\right)\:=\:−\frac{\mathrm{dx}}{\mathrm{y}\left(\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{v}'\left(\mathrm{x}\right)\:+\:\mathrm{v}\left(\mathrm{x}\right)=\:−\mathrm{x} \\ $$$$\mathrm{IF}\:=\:\mathrm{e}^{\int\mathrm{1dx}} =\:\mathrm{e}^{\mathrm{x}} \\ $$$$\mathrm{multiply}\:\mathrm{through}\:\mathrm{by}\:\mathrm{e}^{\mathrm{x}} \\ $$$$\mathrm{e}^{\mathrm{x}} \centerdot\mathrm{v}'\left(\mathrm{x}\right)\:+\:\mathrm{e}^{\mathrm{x}} \centerdot\mathrm{v}\left(\mathrm{x}\right)=\:−\mathrm{xe}^{\mathrm{x}} \\ $$$$\mathrm{substitute}\:\mathrm{e}^{\mathrm{x}} \:=\:\frac{\mathrm{d}\left(\mathrm{e}^{\mathrm{x}} \right)}{\mathrm{dx}}\:\mathrm{and}\:\mathrm{apply}\:\mathrm{the}\:\mathrm{reverse}\:\mathrm{product}\:\mathrm{rule} \\ $$$$\frac{\mathrm{d}\left(\mathrm{e}^{\mathrm{x}} \centerdot\mathrm{v}\left(\mathrm{x}\right)\right)}{\mathrm{dx}}\:=\:−\mathrm{xe}^{\mathrm{x}} \\ $$$$\mathrm{e}^{\mathrm{x}} \centerdot\mathrm{v}\left(\mathrm{x}\right)\:=\:−\mathrm{e}^{\mathrm{x}} \left(\mathrm{x}−\mathrm{1}\right)\:+\:\mathrm{c}_{\mathrm{1}} \\ $$$$\mathrm{v}\left(\mathrm{x}\right)=\:−\left(\mathrm{x}−\mathrm{1}\right)\:+\:\mathrm{c}_{\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \\ $$$$\mathrm{Recall}:\:\mathrm{v}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{y}\left(\mathrm{x}\right)} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} −\mathrm{xe}^{\mathrm{x}} +\mathrm{c}_{\mathrm{1}} } \\ $$
Commented by bramlexs22 last updated on 28/Oct/20
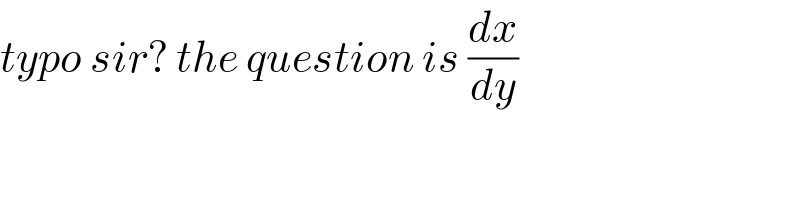
typo sir? the question is (dx/dy)
$${typo}\:{sir}?\:{the}\:{question}\:{is}\:\frac{{dx}}{{dy}} \\ $$
Commented by Lordose last updated on 28/Oct/20
Ohh.
$$\mathrm{Ohh}. \\ $$$$ \\ $$
Commented by Lordose last updated on 28/Oct/20
this is not elementary
$$\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{not}}\:\boldsymbol{\mathrm{elementary}} \\ $$
Commented by bramlexs22 last updated on 28/Oct/20
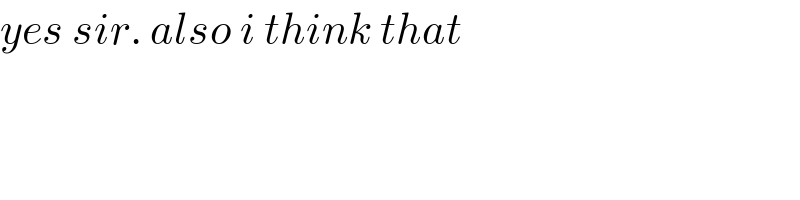
yes sir. also i think that
$${yes}\:{sir}.\:{also}\:{i}\:{think}\:{that} \\ $$
Answered by TANMAY PANACEA last updated on 28/Oct/20
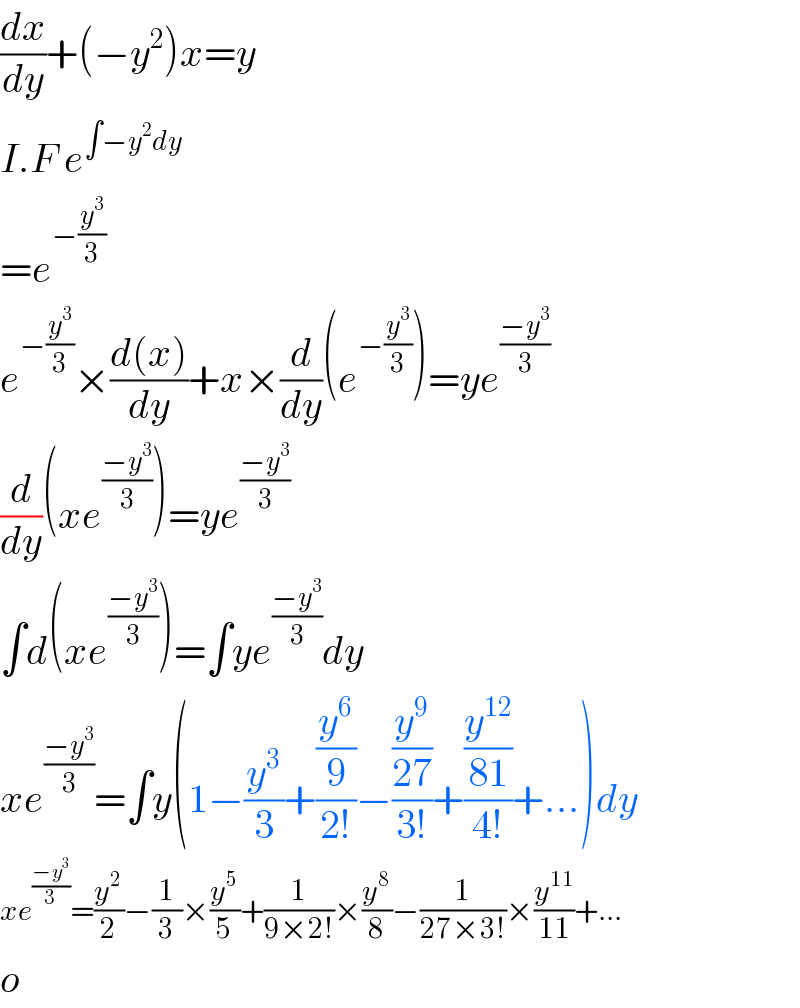
(dx/dy)+(−y^2 )x=y I.F e^(∫−y^2 dy) =e^(−(y^3 /3)) e^(−(y^3 /3)) ×((d(x))/dy)+x×(d/dy)(e^(−(y^3 /3)) )=ye^((−y^3 )/3) (d/dy)(xe^((−y^3 )/3) )=ye^((−y^3 )/3) ∫d(xe^((−y^3 )/3) )=∫ye^((−y^3 )/3) dy xe^((−y^3 )/3) =∫y(1−(y^3 /3)+((y^6 /9)/(2!))−((y^9 /(27))/(3!))+((y^(12) /(81))/(4!))+...)dy xe^((−y^3 )/3) =(y^2 /2)−(1/3)×(y^5 /5)+(1/(9×2!))×(y^8 /8)−(1/(27×3!))×(y^(11) /(11))+... o
$$\frac{{dx}}{{dy}}+\left(−{y}^{\mathrm{2}} \right){x}={y} \\ $$$${I}.{F}\:{e}^{\int−{y}^{\mathrm{2}} {dy}} \\ $$$$={e}^{−\frac{{y}^{\mathrm{3}} }{\mathrm{3}}} \\ $$$${e}^{−\frac{{y}^{\mathrm{3}} }{\mathrm{3}}} ×\frac{{d}\left({x}\right)}{{dy}}+{x}×\frac{{d}}{{dy}}\left({e}^{−\frac{{y}^{\mathrm{3}} }{\mathrm{3}}} \right)={ye}^{\frac{−{y}^{\mathrm{3}} }{\mathrm{3}}} \\ $$$$\frac{{d}}{{dy}}\left({xe}^{\frac{−{y}^{\mathrm{3}} }{\mathrm{3}}} \right)={ye}^{\frac{−{y}^{\mathrm{3}} }{\mathrm{3}}} \\ $$$$\int{d}\left({xe}^{\frac{−{y}^{\mathrm{3}} }{\mathrm{3}}} \right)=\int{ye}^{\frac{−{y}^{\mathrm{3}} }{\mathrm{3}}} {dy} \\ $$$${xe}^{\frac{−{y}^{\mathrm{3}} }{\mathrm{3}}} =\int{y}\left(\mathrm{1}−\frac{{y}^{\mathrm{3}} }{\mathrm{3}}+\frac{\frac{{y}^{\mathrm{6}} }{\mathrm{9}}}{\mathrm{2}!}−\frac{\frac{{y}^{\mathrm{9}} }{\mathrm{27}}}{\mathrm{3}!}+\frac{\frac{{y}^{\mathrm{12}} }{\mathrm{81}}}{\mathrm{4}!}+…\right){dy} \\ $$$${xe}^{\frac{−{y}^{\mathrm{3}} }{\mathrm{3}}} =\frac{{y}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{{y}^{\mathrm{5}} }{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{9}×\mathrm{2}!}×\frac{{y}^{\mathrm{8}} }{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{27}×\mathrm{3}!}×\frac{{y}^{\mathrm{11}} }{\mathrm{11}}+… \\ $$$${o} \\ $$
Commented by bramlexs22 last updated on 28/Oct/20
thank sir
$${thank}\:{sir} \\ $$
Commented by TANMAY PANACEA last updated on 28/Oct/20
most welcome sir
$${most}\:{welcome}\:{sir} \\ $$
Answered by Lordose last updated on 28/Oct/20
(dx/dy)= y(xy+1) y^′ (x)= (1/(y(xy+1))) y′(x) − (1/(y(xy+1))) = 0 multiply by y(xy+1) (dy/dx)y(xy+1) − 1=0 let R(x,y)=−1 and S(x,y) = y(xy+1) This is not an exact equation since (((∂R(x,y))/∂y)=0)≠(y^2 =((∂S(x,y))/∂x)) Let IF = ϕ(y) such that ϕ(y)R(x,y) + (dy/dx)ϕ(y)S(x,y) =0 This implies that ((∂(ϕ(y)R(x,y)))/∂y)=((∂(u(y)S(x,y)))/∂x) ((−d(ϕ(y)))/dy)= y^2 ϕ(y) (((∂(ϕ(y)))/∂y)/(ϕ(y))) = −y^2 Integrating w.r.t y ln(ϕ(y)) = −(y^3 /3) ϕ(y) = e^(−(y^3 /3)) Multiply the original equation by ϕ(y) e^(−(y^3 /3)) y(xy+1)(dy/dx) − e^(−(y^3 /3)) = 0 Let P(x,y)= −e^(−(y^3 /3)) and Q(x,y)=e^(−(y^3 /3)) y(xy+1) Let F(x,y) be such that ((∂F(x,y))/∂x)=P(x,y) and ((∂F(x,y))/∂y)=Q(x,y) Then, the solution required is F(x,y) = c_1 ((∂F(x,y))/∂x)= −e^(−(y^3 /3)) Integrate w.r.t x F(x,y) = −xe^(−(y^3 /3)) + g(y) {g(y) is an arbitrary function of y} ((∂F(x,y))/∂y) = ((∂(−xe^(−(y^3 /3)) +g(y)))/∂y) e^(−(y^3 /3)) y(xy+1) = xy^2 e^(−(y^3 /3)) + ((d(g(y)))/dy) Solving for ((d(g(y)))/dy) {problem for you} ((d(g(y)))/dy) = ye^(−(y^3 /3)) Integrate w.r.t y g(y) = ∫ye^(−(y^3 /3)) dy g(y) = −((𝚪((2/3),(y^3 /3)))/( (3)^(1/3) )) F(x,y) = −xe^(−(y^3 /3)) − ((𝚪((2/3),(y^3 /3)))/( (y)^(1/3) ))
$$ \\ $$$$\frac{\mathrm{dx}}{\mathrm{dy}}=\:\mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right) \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)=\:\frac{\mathrm{1}}{\mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right)} \\ $$$$\mathrm{y}'\left(\mathrm{x}\right)\:−\:\frac{\mathrm{1}}{\mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right)}\:=\:\mathrm{0} \\ $$$$\mathrm{multiply}\:\mathrm{by}\:\mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right)\:−\:\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{R}\left(\mathrm{x},\mathrm{y}\right)=−\mathrm{1}\:\mathrm{and}\:\mathrm{S}\left(\mathrm{x},\mathrm{y}\right)\:=\:\mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right) \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{not}\:\mathrm{an}\:\mathrm{exact}\:\mathrm{equation}\:\mathrm{since}\:\left(\frac{\partial\mathrm{R}\left(\mathrm{x},\mathrm{y}\right)}{\partial\mathrm{y}}=\mathrm{0}\right)\neq\left(\mathrm{y}^{\mathrm{2}} =\frac{\partial\mathrm{S}\left(\mathrm{x},\mathrm{y}\right)}{\partial\mathrm{x}}\right) \\ $$$$\mathrm{Let}\:\mathrm{IF}\:=\:\varphi\left(\mathrm{y}\right)\:\mathrm{such}\:\mathrm{that}\:\varphi\left(\mathrm{y}\right)\mathrm{R}\left(\mathrm{x},\mathrm{y}\right)\:+\:\frac{\mathrm{dy}}{\mathrm{dx}}\varphi\left(\mathrm{y}\right)\mathrm{S}\left(\mathrm{x},\mathrm{y}\right)\:=\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{implies}\:\mathrm{that}\:\frac{\partial\left(\varphi\left(\mathrm{y}\right)\mathrm{R}\left(\mathrm{x},\mathrm{y}\right)\right)}{\partial\mathrm{y}}=\frac{\partial\left(\mathrm{u}\left(\mathrm{y}\right)\mathrm{S}\left(\mathrm{x},\mathrm{y}\right)\right)}{\partial\mathrm{x}} \\ $$$$\frac{−\mathrm{d}\left(\varphi\left(\mathrm{y}\right)\right)}{\mathrm{dy}}=\:\mathrm{y}^{\mathrm{2}} \varphi\left(\mathrm{y}\right) \\ $$$$\frac{\frac{\partial\left(\varphi\left(\mathrm{y}\right)\right)}{\partial\mathrm{y}}}{\varphi\left(\mathrm{y}\right)}\:=\:−\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{Integrating}\:\mathrm{w}.\mathrm{r}.\mathrm{t}\:\mathrm{y} \\ $$$$\mathrm{ln}\left(\varphi\left(\mathrm{y}\right)\right)\:=\:−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\varphi\left(\mathrm{y}\right)\:=\:\mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \\ $$$$\mathrm{Multiply}\:\mathrm{the}\:\mathrm{original}\:\mathrm{equation}\:\mathrm{by}\:\varphi\left(\mathrm{y}\right) \\ $$$$\mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right)\frac{\mathrm{dy}}{\mathrm{dx}}\:−\:\mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} =\:\mathrm{0} \\ $$$$\mathrm{Let}\:\mathrm{P}\left(\mathrm{x},\mathrm{y}\right)=\:−\mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \:\mathrm{and}\:\mathrm{Q}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right) \\ $$$$\mathrm{Let}\:\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{be}\:\mathrm{such}\:\mathrm{that}\:\frac{\partial\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)}{\partial\mathrm{x}}=\mathrm{P}\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{and}\:\frac{\partial\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)}{\partial\mathrm{y}}=\mathrm{Q}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{Then},\:\mathrm{the}\:\mathrm{solution}\:\mathrm{required}\:\mathrm{is}\:\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:\mathrm{c}_{\mathrm{1}} \\ $$$$\frac{\partial\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)}{\partial\mathrm{x}}=\:−\mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \\ $$$$\mathrm{Integrate}\:\mathrm{w}.\mathrm{r}.\mathrm{t}\:\mathrm{x} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:−\mathrm{xe}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} +\:\mathrm{g}\left(\mathrm{y}\right)\:\:\:\:\:\:\:\:\:\:\left\{\mathrm{g}\left(\mathrm{y}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{arbitrary}\:\mathrm{function}\:\mathrm{of}\:\mathrm{y}\right\} \\ $$$$\frac{\partial\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)}{\partial\mathrm{y}}\:=\:\frac{\partial\left(−\mathrm{xe}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} +\mathrm{g}\left(\mathrm{y}\right)\right)}{\partial\mathrm{y}} \\ $$$$\mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \mathrm{y}\left(\mathrm{xy}+\mathrm{1}\right)\:=\:\mathrm{xy}^{\mathrm{2}} \mathrm{e}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \:+\:\frac{\mathrm{d}\left(\mathrm{g}\left(\mathrm{y}\right)\right)}{\mathrm{dy}} \\ $$$$\mathrm{Solving}\:\mathrm{for}\:\frac{\mathrm{d}\left(\mathrm{g}\left(\mathrm{y}\right)\right)}{\mathrm{dy}}\:\:\:\left\{\mathrm{problem}\:\mathrm{for}\:\mathrm{you}\right\} \\ $$$$\frac{\mathrm{d}\left(\mathrm{g}\left(\mathrm{y}\right)\right)}{\mathrm{dy}}\:=\:\mathrm{ye}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \\ $$$$\mathrm{Integrate}\:\mathrm{w}.\mathrm{r}.\mathrm{t}\:\mathrm{y} \\ $$$$\mathrm{g}\left(\mathrm{y}\right)\:=\:\int\mathrm{ye}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} \mathrm{dy} \\ $$$$\mathrm{g}\left(\mathrm{y}\right)\:=\:−\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}\right)}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:=\:−\mathrm{xe}^{−\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}} −\:\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}\right)}{\:\sqrt[{\mathrm{3}}]{\mathrm{y}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *