Question Number 144716 by mathdanisur last updated on 28/Jun/21
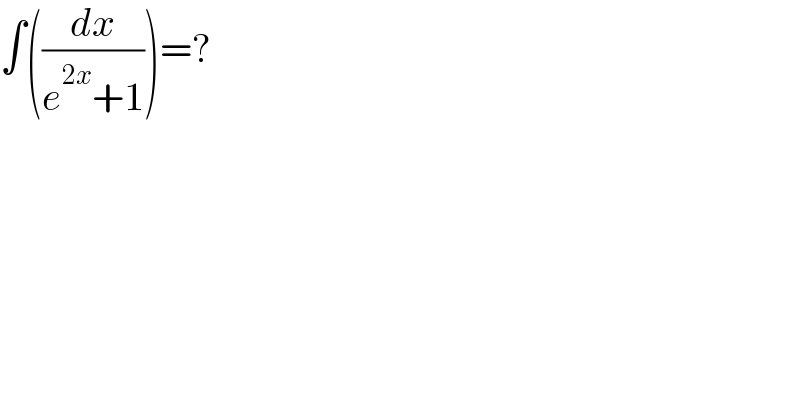
$$\int\left(\frac{{dx}}{{e}^{\mathrm{2}{x}} +\mathrm{1}}\right)=? \\ $$
Answered by imjagoll last updated on 28/Jun/21
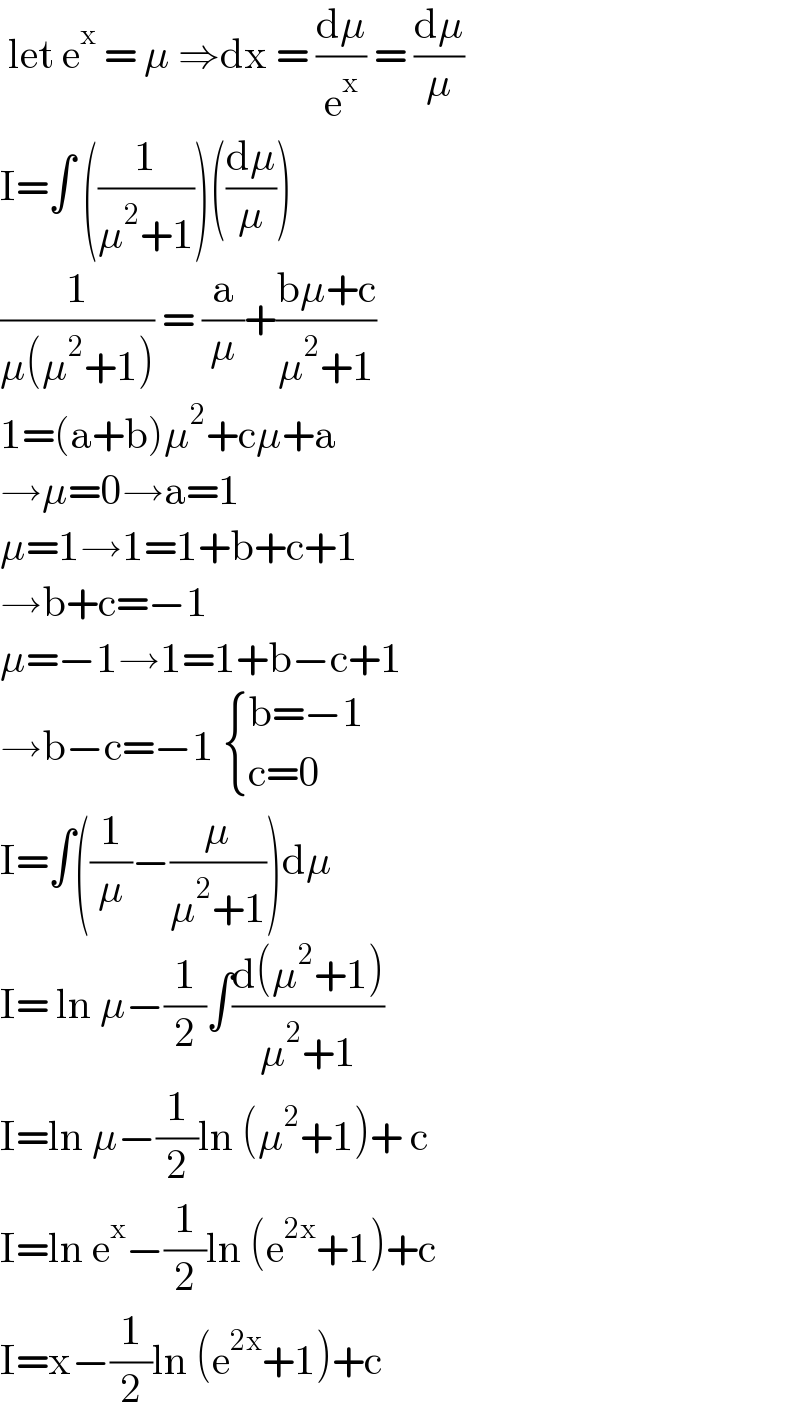
$$\:\mathrm{let}\:\mathrm{e}^{\mathrm{x}} \:=\:\mu\:\Rightarrow\mathrm{dx}\:=\:\frac{\mathrm{d}\mu}{\mathrm{e}^{\mathrm{x}} }\:=\:\frac{\mathrm{d}\mu}{\mu} \\ $$$$\mathrm{I}=\int\:\left(\frac{\mathrm{1}}{\mu^{\mathrm{2}} +\mathrm{1}}\right)\left(\frac{\mathrm{d}\mu}{\mu}\right) \\ $$$$\frac{\mathrm{1}}{\mu\left(\mu^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\frac{\mathrm{a}}{\mu}+\frac{\mathrm{b}\mu+\mathrm{c}}{\mu^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{1}=\left(\mathrm{a}+\mathrm{b}\right)\mu^{\mathrm{2}} +\mathrm{c}\mu+\mathrm{a} \\ $$$$\rightarrow\mu=\mathrm{0}\rightarrow\mathrm{a}=\mathrm{1} \\ $$$$\mu=\mathrm{1}\rightarrow\mathrm{1}=\mathrm{1}+\mathrm{b}+\mathrm{c}+\mathrm{1} \\ $$$$\rightarrow\mathrm{b}+\mathrm{c}=−\mathrm{1} \\ $$$$\mu=−\mathrm{1}\rightarrow\mathrm{1}=\mathrm{1}+\mathrm{b}−\mathrm{c}+\mathrm{1} \\ $$$$\rightarrow\mathrm{b}−\mathrm{c}=−\mathrm{1}\:\begin{cases}{\mathrm{b}=−\mathrm{1}}\\{\mathrm{c}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{I}=\int\left(\frac{\mathrm{1}}{\mu}−\frac{\mu}{\mu^{\mathrm{2}} +\mathrm{1}}\right)\mathrm{d}\mu \\ $$$$\mathrm{I}=\:\mathrm{ln}\:\mu−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mu^{\mathrm{2}} +\mathrm{1}\right)}{\mu^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{I}=\mathrm{ln}\:\mu−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mu^{\mathrm{2}} +\mathrm{1}\right)+\:\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{ln}\:\mathrm{e}^{\mathrm{x}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{2x}} +\mathrm{1}\right)+\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{2x}} +\mathrm{1}\right)+\mathrm{c}\: \\ $$
Commented by mathdanisur last updated on 28/Jun/21

$${thanks}\:{Sir}\:{cool} \\ $$
