Question Number 118094 by bemath last updated on 15/Oct/20
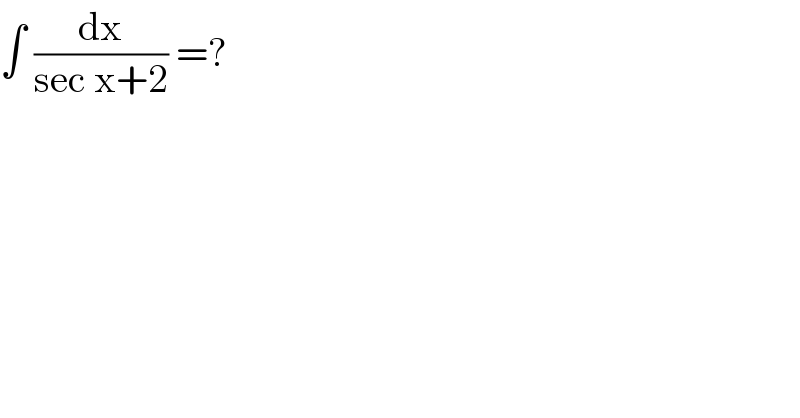
$$\int\:\frac{\mathrm{dx}}{\mathrm{sec}\:\mathrm{x}+\mathrm{2}}\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 15/Oct/20
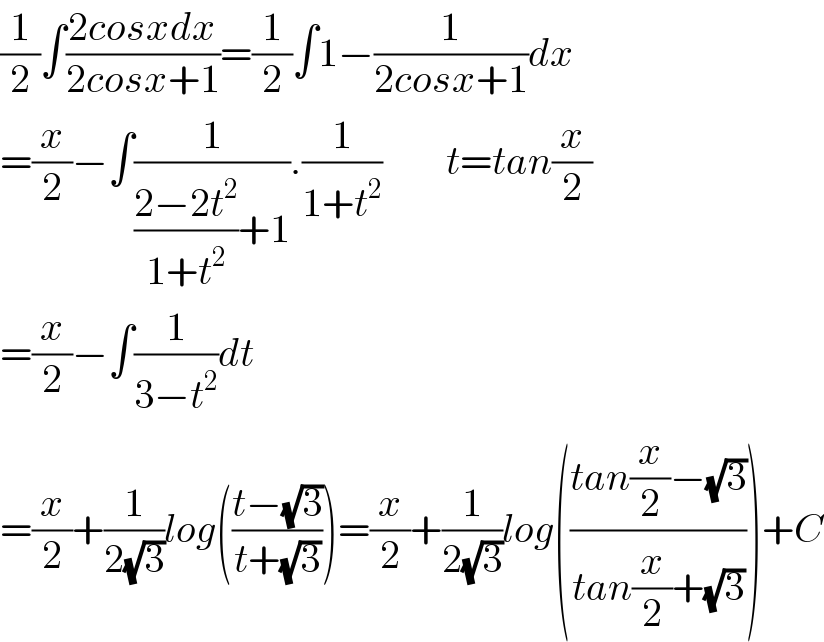
$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{cosxdx}}{\mathrm{2}{cosx}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{cosx}+\mathrm{1}}{dx} \\ $$$$=\frac{{x}}{\mathrm{2}}−\int\frac{\mathrm{1}}{\frac{\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{1}}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:\:\:\:\:\:{t}={tan}\frac{{x}}{\mathrm{2}} \\ $$$$=\frac{{x}}{\mathrm{2}}−\int\frac{\mathrm{1}}{\mathrm{3}−{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{log}\left(\frac{{t}−\sqrt{\mathrm{3}}}{{t}+\sqrt{\mathrm{3}}}\right)=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{log}\left(\frac{{tan}\frac{{x}}{\mathrm{2}}−\sqrt{\mathrm{3}}}{{tan}\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{3}}}\right)+{C} \\ $$
Commented by bemath last updated on 15/Oct/20

$$\mathrm{weirstrass}\:\mathrm{substitution} \\ $$$$\mathrm{santuy}… \\ $$
