dx-sec-x-csc-x-

Question Number 82185 by jagoll last updated on 19/Feb/20

$$\int\:\frac{{dx}}{\mathrm{sec}\:{x}\:+\:{csc}\:{x}}\:=\:?\: \\ $$

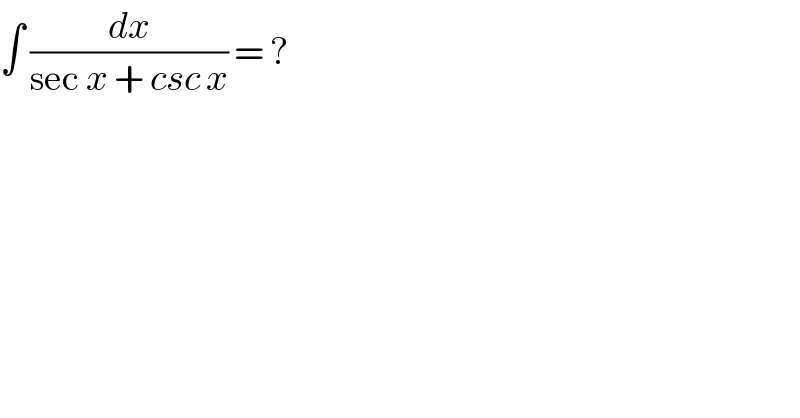
Commented by john santu last updated on 19/Feb/20

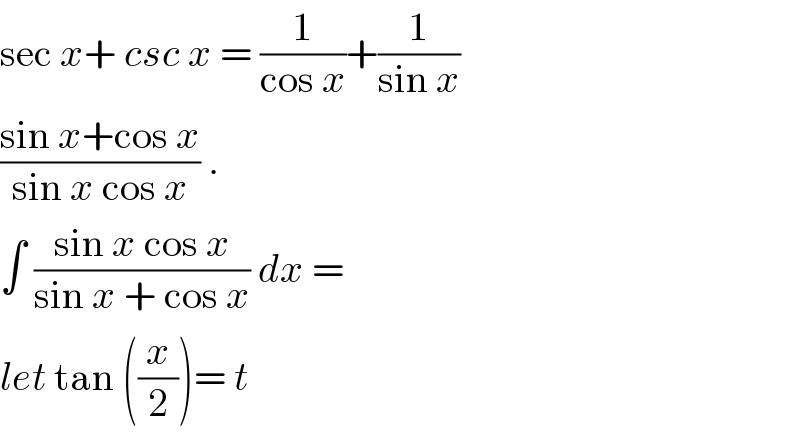
sec x+ csc x = (1/(cos x))+(1/(sin x)) ((sin x+cos x)/(sin x cos x)) . ∫ ((sin x cos x)/(sin x + cos x)) dx = let tan ((x/2))= t

$$\mathrm{sec}\:{x}+\:{csc}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:{x}}+\frac{\mathrm{1}}{\mathrm{sin}\:{x}} \\ $$$$\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}\:. \\ $$$$\int\:\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x}}\:{dx}\:=\: \\ $$$${let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)=\:{t}\: \\ $$

Commented by mathmax by abdo last updated on 19/Feb/20

let I =∫ (dx/((1/(cosx)) +(1/(sinx)))) ⇒I =∫ ((cosx .sinx)/(cosx +sinx))dx changement tan((x/2))=t give I =∫ ((((1−t^2 )/(1+t^2 ))×((2t)/(1+t^2 )))/(((1−t^2 )/(1+t^2 ))+((2t)/(1+t^2 ))))×((2dt)/(1+t^2 )) =∫((2t(1−t^2 ))/((1+t^2 )^2 (−t^2 +2t+1)))dt =∫ ((2t(t^2 −1))/((t^2 +1)^2 (t^2 −2t−1)))dt =∫ ((2t^3 −2t)/((t^2 +1)^2 (t^2 −2t −1)))dt t^2 −2t−1 =0→Δ^′ =1+1=2 ⇒t_1 =1+(√2)and t_2 =1−(√2) let decompose F(t)=((2t^3 −2t)/((t^2 +1)^2 (t−t_1 )(t−t_2 ))) ⇒F(t)=(a/(t−t_1 )) +(b/(t−t_2 )) +((ct +d)/(t^2 +1)) +((et +f)/((t^2 +1)^2 )) ⇒∫ F(t)dt =aln∣t−t_1 ∣+bln∣t−t_2 ∣ +(c/2)ln(t^2 +1)+d arctan(t) +∫ ((et +f)/((t^2 +1)^2 ))dt rest calculus of coefficients ...be continued...

$${let}\:\:{I}\:=\int\:\:\:\frac{{dx}}{\frac{\mathrm{1}}{{cosx}}\:+\frac{\mathrm{1}}{{sinx}}}\:\Rightarrow{I}\:=\int\:\:\frac{{cosx}\:.{sinx}}{{cosx}\:+{sinx}}{dx}\:\:{changement} \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\:{I}\:=\int\:\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\frac{\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left(−{t}^{\mathrm{2}} \:+\mathrm{2}{t}+\mathrm{1}\right)}{dt} \\ $$$$=\int\:\:\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)}{dt}\:=\int\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}\:−\mathrm{1}\right)}{dt} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\:=\mathrm{0}\rightarrow\Delta^{'} =\mathrm{1}+\mathrm{1}=\mathrm{2}\:\Rightarrow{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}{and}\:{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}}\:\:{let}\:{decompose} \\ $$$${F}\left({t}\right)=\frac{\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)}\:\Rightarrow{F}\left({t}\right)=\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{et}\:+{f}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\int\:{F}\left({t}\right){dt}\:={aln}\mid{t}−{t}_{\mathrm{1}} \mid+{bln}\mid{t}−{t}_{\mathrm{2}} \mid\:+\frac{{c}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)+{d}\:{arctan}\left({t}\right) \\ $$$$+\int\:\frac{{et}\:+{f}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt}\:\:{rest}\:{calculus}\:{of}\:{coefficients}\:…{be}\:{continued}… \\ $$$$ \\ $$

Answered by TANMAY PANACEA last updated on 20/Feb/20

∫((sinx+cosx)/(sinxcosx))dx 2∫((sinx+cosx)/(1−(1−2sinxcosx)))dx 2∫((d(sinx−cosx))/(1−(sinx−cosx)^2 )) [formula ∫(da/(1−a^2 ))] ln(((sinx−cosx+1)/(sinx−cosx−1)))+c

$$\int\frac{{sinx}+{cosx}}{{sinxcosx}}{dx} \\ $$$$\mathrm{2}\int\frac{{sinx}+{cosx}}{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}{sinxcosx}\right)}{dx} \\ $$$$\mathrm{2}\int\frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{1}−\left({sinx}−{cosx}\right)^{\mathrm{2}} }\:\left[{formula}\:\int\frac{{da}}{\mathrm{1}−{a}^{\mathrm{2}} }\right] \\ $$$${ln}\left(\frac{{sinx}−{cosx}+\mathrm{1}}{{sinx}−{cosx}−\mathrm{1}}\right)+{c} \\ $$

Commented by jagoll last updated on 20/Feb/20

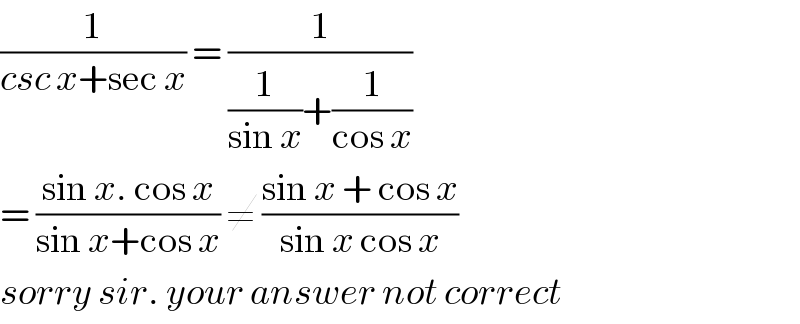
(1/(csc x+sec x)) = (1/((1/(sin x))+(1/(cos x)))) = ((sin x. cos x)/(sin x+cos x)) ≠ ((sin x + cos x)/(sin x cos x)) sorry sir. your answer not correct

$$\frac{\mathrm{1}}{{csc}\:{x}+\mathrm{sec}\:{x}}\:=\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{x}}} \\ $$$$=\:\frac{\mathrm{sin}\:{x}.\:\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:\neq\:\frac{\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}} \\ $$$${sorry}\:{sir}.\:{your}\:{answer}\:{not}\:{correct} \\ $$

Commented by TANMAY PANACEA last updated on 20/Feb/20

Facebook Tweet Pin

Leave a Reply Cancel reply