Question Number 170926 by Tawa11 last updated on 04/Jun/22
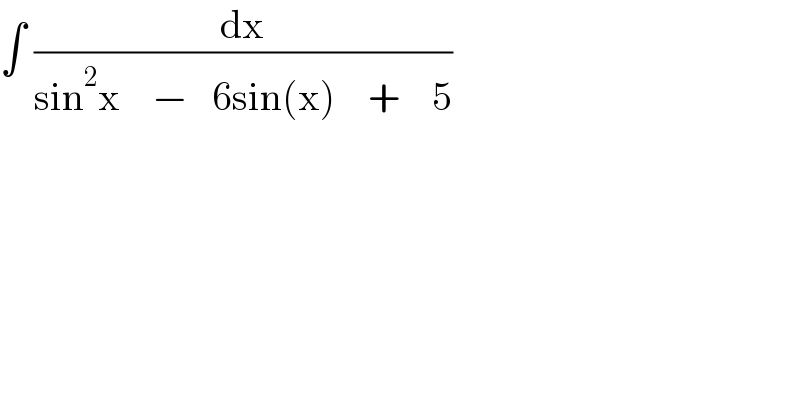
$$\int\:\frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\:\:\:−\:\:\:\mathrm{6sin}\left(\mathrm{x}\right)\:\:\:\:+\:\:\:\:\mathrm{5}} \\ $$
Answered by thfchristopher last updated on 04/Jun/22
![∫(dx/(sin^2 x−6sin x+5)) Let t=tan(x/2) ⇒ sin x=((2t)/(1+t^2 )) dt=(1/2)sec^2 (x/2)dx ⇒ dx=((2dt)/(1+t^2 )) ∴ ∫(dx/(sin^2 x−6sin x+5)) =∫(((2dt)/(1+t^2 ))/((((2t)/(1+t^2 )))^2 −6(((2t)/(1+t^2 )))+5)) =∫((2(1+t^2 ))/(4t^2 −12t(1+t^2 )+5(1+t^2 )^2 ))dt =∫((2(1+t^2 ))/(5t^4 −12t^3 +14t^2 −12t+5))dt =∫((2(1+t^2 ))/((t−1)^2 (5t^2 −2t+5)))dt =(1/2)∫[(1/((t−1)^2 ))−(1/(5t^2 −2t+5))]dt =(1/2)∫(dt/((t−1)^2 ))−(1/(10))∫(dt/(t^2 −(2/5)t+1)) =(1/(2(1−t)))−(1/(10))∫(dt/((t−(1/5))^2 +(((2(√6))/5))^2 )) For ∫(dt/((t−(1/5))^2 +(((2(√6))/5))^2 )) , Let t−(1/5)=((2(√6))/5)tan u, dt=((2(√6))/5)sec^2 udu ∴ ∫(dt/((t−(1/5))^2 +(((2(√6))/5))^2 )) =(5/(2(√6)))∫((sec^2 u)/(sec^2 u))du =(5/(2(√6)))∫du = (5/(2(√6)))u+C =(5/(2(√6)))tan^(−1) (((5t−1)/(2(√6))))+C Hence, ∫(dx/(sin^2 x−6sin x+5)) =(1/(2(1−t)))−(1/(4(√6)))tan^(−1) (((5t−1)/(2(√6))))+C =(1/(2[1−tan (x/2)]))−(1/(4(√6)))tan^(−1) [((5tan ((x/2))−1)/(2(√6)))]+C](https://www.tinkutara.com/question/Q170955.png)
$$\int\frac{{dx}}{\mathrm{sin}^{\mathrm{2}} {x}−\mathrm{6sin}\:{x}+\mathrm{5}} \\ $$$$\mathrm{Let}\:{t}=\mathrm{tan}\frac{{x}}{\mathrm{2}}\:\Rightarrow\:\mathrm{sin}\:{x}=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${dt}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}\:\Rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\therefore\:\int\frac{{dx}}{\mathrm{sin}^{\mathrm{2}} {x}−\mathrm{6sin}\:{x}+\mathrm{5}} \\ $$$$=\int\frac{\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{6}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)+\mathrm{5}} \\ $$$$=\int\frac{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{4}{t}^{\mathrm{2}} −\mathrm{12}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\mathrm{5}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\int\frac{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{5}{t}^{\mathrm{4}} −\mathrm{12}{t}^{\mathrm{3}} +\mathrm{14}{t}^{\mathrm{2}} −\mathrm{12}{t}+\mathrm{5}}{dt} \\ $$$$=\int\frac{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{5}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{5}\right)}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left[\frac{\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{5}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{5}}\right]{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{5}}{t}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{t}\right)}−\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{For}\:\int\frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}}\right)^{\mathrm{2}} }\:, \\ $$$$\mathrm{Let}\:{t}−\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}}\mathrm{tan}\:{u}, \\ $$$${dt}=\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}}\mathrm{sec}^{\mathrm{2}} {udu} \\ $$$$\therefore\:\int\frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}}\int\frac{\cancel{\mathrm{sec}^{\mathrm{2}} {u}}}{\cancel{\mathrm{sec}^{\mathrm{2}} {u}}}{du} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}}\int{du} \\ $$$$=\:\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}}{u}+{C} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}{t}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\right)+{C} \\ $$$$\mathrm{Hence}, \\ $$$$\int\frac{{dx}}{\mathrm{sin}^{\mathrm{2}} {x}−\mathrm{6sin}\:{x}+\mathrm{5}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{t}\right)}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}{t}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left[\mathrm{1}−\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right]}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{5tan}\:\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\right]+{C} \\ $$
Commented by Tawa11 last updated on 04/Jun/22

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by peter frank last updated on 05/Jun/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mr W last updated on 05/Jun/22
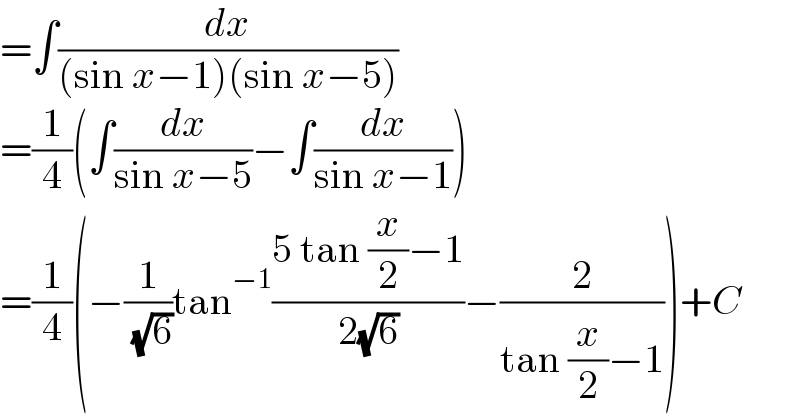
$$=\int\frac{{dx}}{\left(\mathrm{sin}\:{x}−\mathrm{1}\right)\left(\mathrm{sin}\:{x}−\mathrm{5}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\int\frac{{dx}}{\mathrm{sin}\:{x}−\mathrm{5}}−\int\frac{{dx}}{\mathrm{sin}\:{x}−\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{5}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}−\frac{\mathrm{2}}{\mathrm{tan}\:\frac{{x}}{\mathrm{2}}−\mathrm{1}}\right)+{C} \\ $$
Commented by Tawa11 last updated on 05/Jun/22

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
