Menu Close

dx-sin-3-2x-cos-3-2x-

Tinku Tara 0 Comments
Pin




Question Number 89318 by M±th+et£s last updated on 16/Apr/20
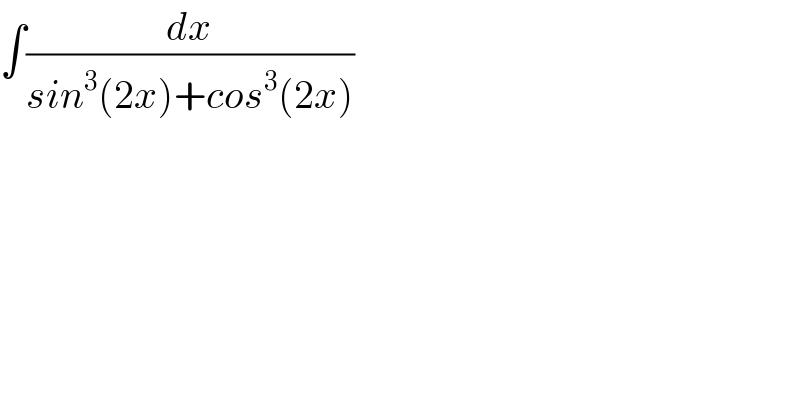
∫(dx/(sin^3 (2x)+cos^3 (2x)))
$$\int\frac{{dx}}{{sin}^{\mathrm{3}} \left(\mathrm{2}{x}\right)+{cos}^{\mathrm{3}} \left(\mathrm{2}{x}\right)} \\ $$
Answered by MJS last updated on 16/Apr/20
∫(dx/(sin^3 2x +cos^3 2x))= [t=tan x → dx=cos^2 x dt] =−∫(((t^2 +1)^2 )/((t^2 −2t−1)(t^2 +(1−(√3))t+2−(√3))(t^2 +(1+(√3))t+2+(√3))))dt= =−(2/3)∫(dt/(t^2 −2t−1))+ −((1−(√3))/6)∫(dt/(t^2 +(1−(√3))t+2−(√3)))− −((1+(√3))/6)∫(dt/(t^2 +(1+(√3))t+2+(√3)))= [now use formulas] =((√2)/6)ln ((t−1+(√2))/(t−1−(√2))) +(1/3)(arctan ((1+(√3))t−1) +arctan ((1−(√3))t−1)) with t=tan x
$$\int\frac{{dx}}{\mathrm{sin}^{\mathrm{3}} \:\mathrm{2}{x}\:+\mathrm{cos}^{\mathrm{3}} \:\mathrm{2}{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=−\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}\right)}{dt}= \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}+ \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}}− \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}}= \\ $$$$\left[\mathrm{now}\:\mathrm{use}\:\mathrm{formulas}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\mathrm{ln}\:\frac{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{arctan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}−\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}−\mathrm{1}\right)\right) \\ $$$$\mathrm{with}\:{t}=\mathrm{tan}\:{x} \\ $$
Commented by M±th+et£s last updated on 16/Apr/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by M±th+et£s last updated on 17/Apr/20
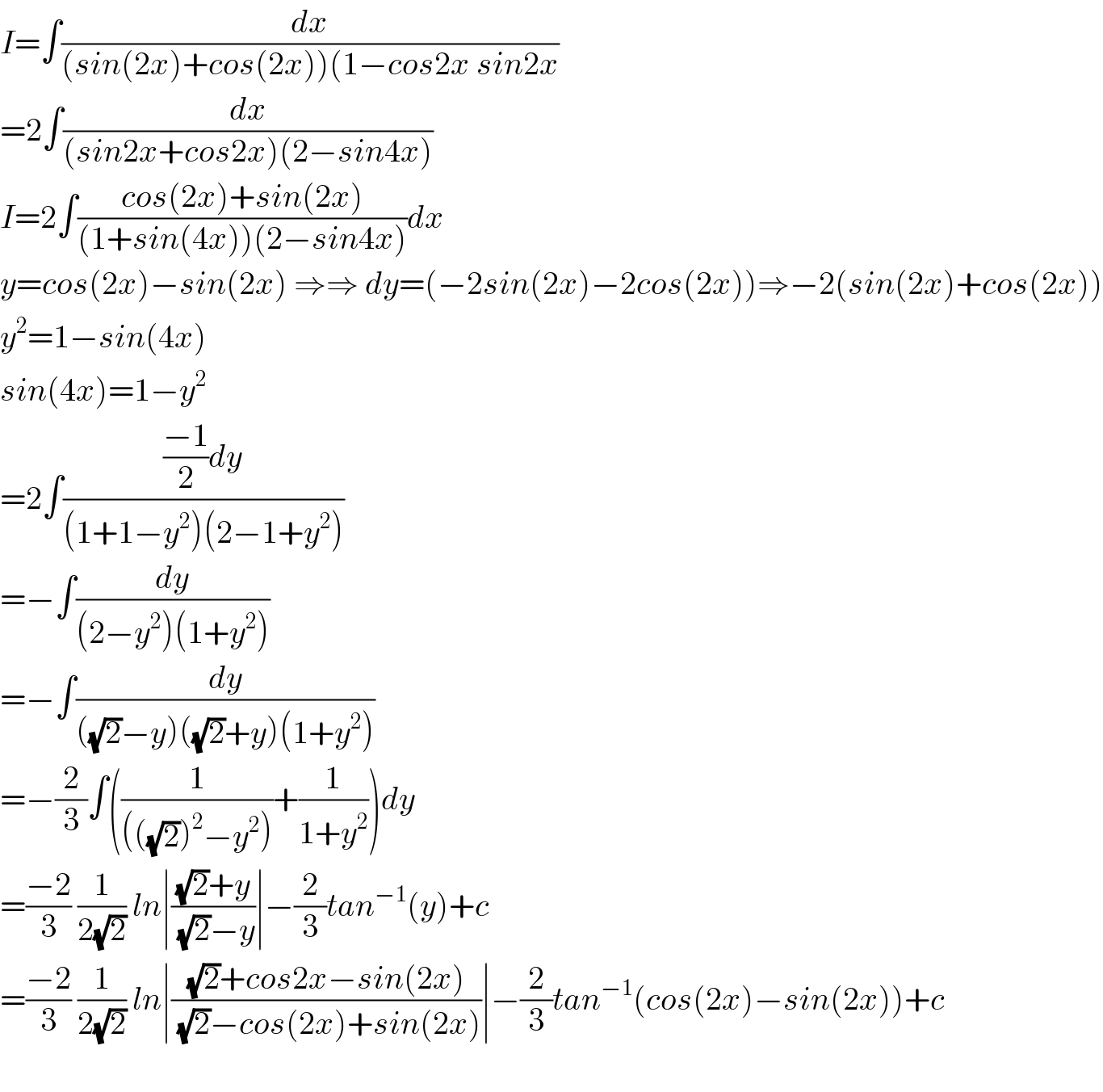
I=∫(dx/((sin(2x)+cos(2x))(1−cos2x sin2x)) =2∫(dx/((sin2x+cos2x)(2−sin4x))) I=2∫((cos(2x)+sin(2x))/((1+sin(4x))(2−sin4x)))dx y=cos(2x)−sin(2x) ⇒⇒ dy=(−2sin(2x)−2cos(2x))⇒−2(sin(2x)+cos(2x)) y^2 =1−sin(4x) sin(4x)=1−y^2 =2∫((((−1)/2)dy)/((1+1−y^2 )(2−1+y^2 ))) =−∫(dy/((2−y^2 )(1+y^2 ))) =−∫(dy/(((√2)−y)((√2)+y)(1+y^2 ))) =−(2/3)∫((1/((((√2))^2 −y^2 )))+(1/(1+y^2 )))dy =((−2)/3) (1/(2(√2))) ln∣(((√2)+y)/( (√2)−y))∣−(2/3)tan^(−1) (y)+c =((−2)/3) (1/(2(√2))) ln∣(((√2)+cos2x−sin(2x))/( (√2)−cos(2x)+sin(2x)))∣−(2/3)tan^(−1) (cos(2x)−sin(2x))+c
$${I}=\int\frac{{dx}}{\left({sin}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{2}{x}\right)\right)\left(\mathrm{1}−{cos}\mathrm{2}{x}\:{sin}\mathrm{2}{x}\right.} \\ $$$$=\mathrm{2}\int\frac{{dx}}{\left({sin}\mathrm{2}{x}+{cos}\mathrm{2}{x}\right)\left(\mathrm{2}−{sin}\mathrm{4}{x}\right)} \\ $$$${I}=\mathrm{2}\int\frac{{cos}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{2}{x}\right)}{\left(\mathrm{1}+{sin}\left(\mathrm{4}{x}\right)\right)\left(\mathrm{2}−{sin}\mathrm{4}{x}\right)}{dx} \\ $$$${y}={cos}\left(\mathrm{2}{x}\right)−{sin}\left(\mathrm{2}{x}\right)\:\Rightarrow\Rightarrow\:{dy}=\left(−\mathrm{2}{sin}\left(\mathrm{2}{x}\right)−\mathrm{2}{cos}\left(\mathrm{2}{x}\right)\right)\Rightarrow−\mathrm{2}\left({sin}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{2}{x}\right)\right) \\ $$$${y}^{\mathrm{2}} =\mathrm{1}−{sin}\left(\mathrm{4}{x}\right) \\ $$$${sin}\left(\mathrm{4}{x}\right)=\mathrm{1}−{y}^{\mathrm{2}} \\ $$$$=\mathrm{2}\int\frac{\frac{−\mathrm{1}}{\mathrm{2}}{dy}}{\left(\mathrm{1}+\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{2}−\mathrm{1}+{y}^{\mathrm{2}} \right)} \\ $$$$=−\int\frac{{dy}}{\left(\mathrm{2}−{y}^{\mathrm{2}} \right)\left(\mathrm{1}+{y}^{\mathrm{2}} \right)} \\ $$$$=−\int\frac{{dy}}{\left(\sqrt{\mathrm{2}}−{y}\right)\left(\sqrt{\mathrm{2}}+{y}\right)\left(\mathrm{1}+{y}^{\mathrm{2}} \right)} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\int\left(\frac{\mathrm{1}}{\left(\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −{y}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} }\right){dy} \\ $$$$=\frac{−\mathrm{2}}{\mathrm{3}}\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:{ln}\mid\frac{\sqrt{\mathrm{2}}+{y}}{\:\sqrt{\mathrm{2}}−{y}}\mid−\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left({y}\right)+{c} \\ $$$$=\frac{−\mathrm{2}}{\mathrm{3}}\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:{ln}\mid\frac{\sqrt{\mathrm{2}}+{cos}\mathrm{2}{x}−{sin}\left(\mathrm{2}{x}\right)}{\:\sqrt{\mathrm{2}}−{cos}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{2}{x}\right)}\mid−\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left({cos}\left(\mathrm{2}{x}\right)−{sin}\left(\mathrm{2}{x}\right)\right)+{c} \\ $$$$ \\ $$
Commented by MJS last updated on 17/Apr/20
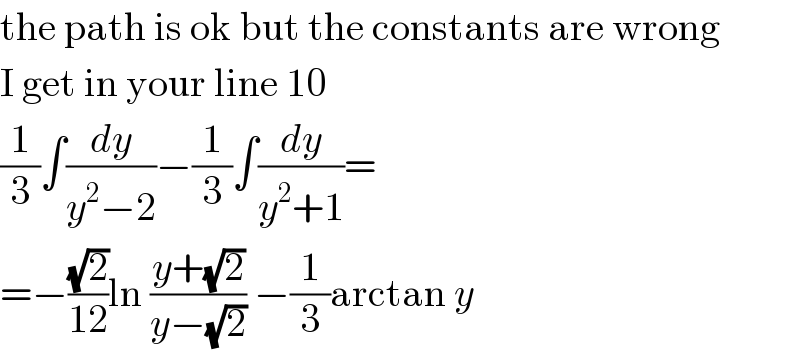
the path is ok but the constants are wrong I get in your line 10 (1/3)∫(dy/(y^2 −2))−(1/3)∫(dy/(y^2 +1))= =−((√2)/(12))ln ((y+(√2))/(y−(√2))) −(1/3)arctan y
$$\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{ok}\:\mathrm{but}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{are}\:\mathrm{wrong} \\ $$$$\mathrm{I}\:\mathrm{get}\:\mathrm{in}\:\mathrm{your}\:\mathrm{line}\:\mathrm{10} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dy}}{{y}^{\mathrm{2}} −\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dy}}{{y}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\mathrm{ln}\:\frac{{y}+\sqrt{\mathrm{2}}}{{y}−\sqrt{\mathrm{2}}}\:−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:{y} \\ $$
Commented by M±th+et£s last updated on 17/Apr/20
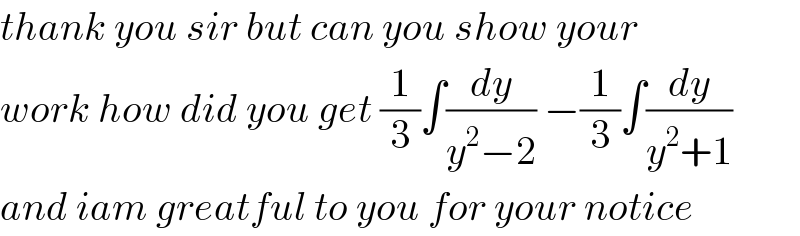
thank you sir but can you show your work how did you get (1/3)∫(dy/(y^2 −2)) −(1/3)∫(dy/(y^2 +1)) and iam greatful to you for your notice
$${thank}\:{you}\:{sir}\:{but}\:{can}\:{you}\:{show}\:{your} \\ $$$${work}\:{how}\:{did}\:{you}\:{get}\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dy}}{{y}^{\mathrm{2}} −\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dy}}{{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$${and}\:{iam}\:{greatful}\:{to}\:{you}\:{for}\:{your}\:{notice} \\ $$
Commented by M±th+et£s last updated on 17/Apr/20
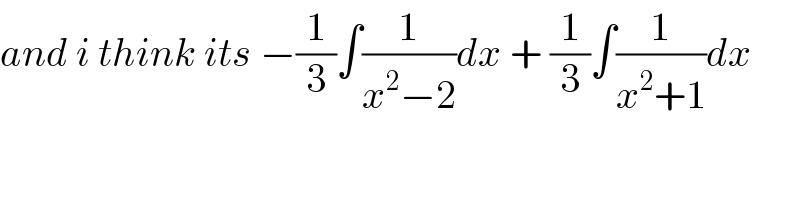
and i think its −(1/3)∫(1/(x^2 −2))dx + (1/3)∫(1/(x^2 +1))dx
$${and}\:{i}\:{think}\:{its}\:−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}}{dx}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$
Commented by M±th+et£s last updated on 17/Apr/20
ok sir thank you i get it
$${ok}\:{sir}\:{thank}\:{you}\:{i}\:{get}\:{it} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *