Question Number 87046 by Tajaddin last updated on 02/Apr/20
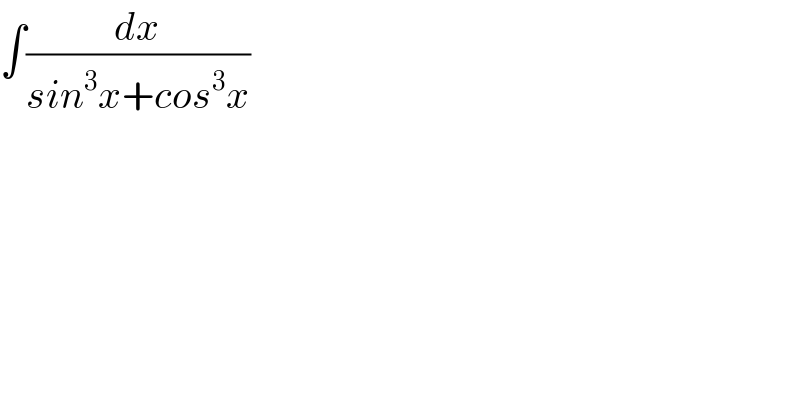
$$\int\frac{{dx}}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}} \\ $$
Answered by MJS last updated on 02/Apr/20
![∫(dx/(sin^3 x +cos^3 x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−2∫((t^4 +2t^2 +1)/(t^6 −3t^4 −8t^3 +3t^2 −1))dt= =−2∫(((t^2 +1)^2 )/((t^2 −2t−1)(t^4 +2t^3 +2t^2 −2t+1)))dt= =−2∫(((t^2 +1)^2 )/((t^2 −1−(√2))(t−1+(√2))(t^2 +(1−(√3))t+2−(√3))(t^2 +(1+(√3))t+2+(√3))))dt= =−((√2)/3)∫(dt/(t−1−(√2)))+((√2)/3)∫(dt/(t−1+(√2)))− −((1−(√3))/3)∫(dt/(t^2 +(1−(√3))t+2−(√3)))− −((1+(√3))/3)∫(dt/(t^2 +(1+(√3))t+2+(√3)))= [now using formula] =((√2)/3)ln ((t−1+(√2))/(t−1−(√2))) +(2/3)(arctan ((1+(√3))t−1) +arctan ((1−(√3))t−1) now insert t=tan (x/2)](https://www.tinkutara.com/question/Q87053.png)
$$\int\frac{{dx}}{\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{cos}^{\mathrm{3}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{6}} −\mathrm{3}{t}^{\mathrm{4}} −\mathrm{8}{t}^{\mathrm{3}} +\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}}{dt}= \\ $$$$=−\mathrm{2}\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)}{dt}= \\ $$$$=−\mathrm{2}\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}−\sqrt{\mathrm{2}}\right)\left({t}−\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}\right)}{dt}= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\int\frac{{dt}}{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\int\frac{{dt}}{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}− \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}}− \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}}= \\ $$$$\:\:\:\:\:\left[\mathrm{now}\:\mathrm{using}\:\mathrm{formula}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{ln}\:\frac{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}\:+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{arctan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}−\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}−\mathrm{1}\right)\right. \\ $$$$\mathrm{now}\:\mathrm{insert}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 02/Apr/20
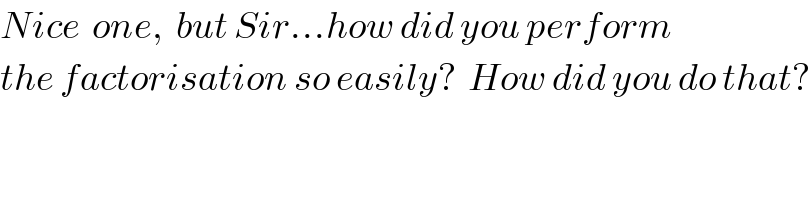
$${Nice}\:\:{one},\:\:{but}\:{Sir}…{how}\:{did}\:{you}\:{perform} \\ $$$${the}\:{factorisation}\:{so}\:{easily}?\:\:{How}\:{did}\:{you}\:{do}\:{that}? \\ $$
