Question Number 125187 by bemath last updated on 08/Dec/20
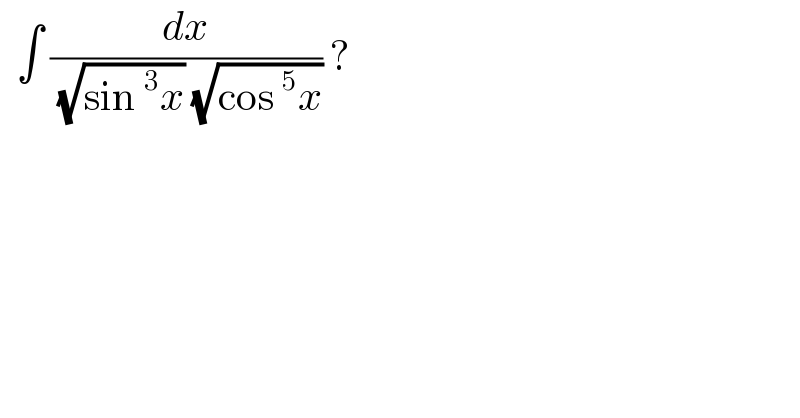
$$\:\:\int\:\frac{{dx}}{\:\sqrt{\mathrm{sin}\:^{\mathrm{3}} {x}}\:\sqrt{\mathrm{cos}\:^{\mathrm{5}} {x}}}\:? \\ $$
Answered by liberty last updated on 08/Dec/20

$${I}=\int\:\sqrt{\frac{\left(\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{3}} {x}}\right)}{\mathrm{tan}\:^{\mathrm{3}} {x}\:\mathrm{cos}\:^{\mathrm{5}} {x}}}\:{dx}\:=\:\int\frac{{dx}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{3}} {x}}\:\sqrt{\mathrm{cos}\:^{\mathrm{8}} {x}}} \\ $$$${I}\:=\:\int\:\frac{\mathrm{sec}\:^{\mathrm{4}} {x}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{3}} {x}}}\:{dx}\:=\:\int\:\frac{\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)\:\mathrm{sec}\:^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{3}} {x}}}\:{dx} \\ $$$${letting}\:\mathrm{tan}\:{x}\:=\:{p}\:\Rightarrow\:\mathrm{sec}\:^{\mathrm{2}} {x}\:{dx}\:=\:{dp} \\ $$$${I}=\int\frac{\left(\mathrm{1}+{p}^{\mathrm{2}} \right)}{{p}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{dp}\:=\:\int\:\left({p}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:+\:{p}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\:{dp} \\ $$$${I}=\:−\mathrm{2}{p}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:+\:\frac{\mathrm{2}}{\mathrm{3}}{p}^{\frac{\mathrm{3}}{\mathrm{2}}} \:+\:{c}\: \\ $$$${I}\:=\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{tan}\:{x}}}\:+\:\frac{\mathrm{2}\sqrt{\mathrm{tan}\:^{\mathrm{3}} {x}}}{\mathrm{3}}\:+\:{c}\: \\ $$
