Question Number 166320 by bobhans last updated on 18/Feb/22
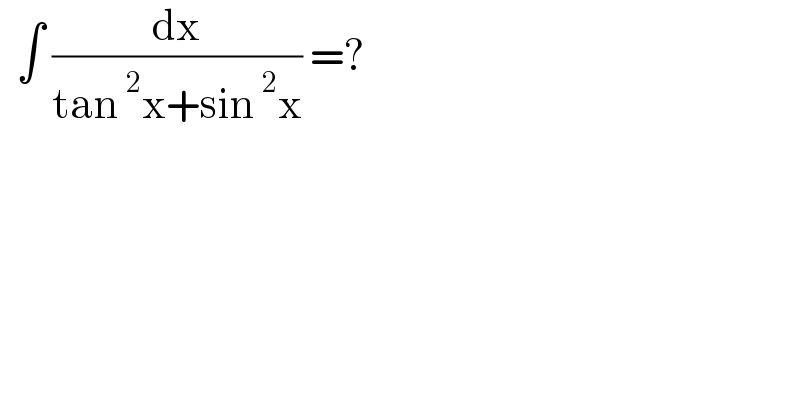
$$\:\:\int\:\frac{\mathrm{dx}}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:=? \\ $$
Answered by cortano1 last updated on 18/Feb/22
![Y=∫ (dx/(tan^2 x+sin^2 x)) =? Y=∫ ((sec^2 x)/(sec^2 x(tan^2 x+sin^2 x))) dx Y=∫ ((sec^2 x)/(sec^2 x tan^2 x+tan^2 x)) dx Y=∫ ((sec^2 x)/(tan^2 x(sec^2 x+1))) dx Y= ∫((d(tan x))/(tan^2 x(2+tan^2 x))) Y= ∫ (dy/(y^2 (2+y^2 ))) ; [ y=tan x ] Y=∫ (1/2)((1/y^2 )−(1/(2+y^2 )))dy Y=(1/2)∫(y^(−2) −(1/(((√2))^2 +y^2 )))dy Y=−(1/(2y))−(1/2).(1/( (√2)))arctan ((y/( (√2))))+c Y=−(1/(2tan x))−((√2)/4)arctan (((tan x)/( (√2))))+ c](https://www.tinkutara.com/question/Q166322.png)
$$\:\mathrm{Y}=\int\:\frac{\mathrm{dx}}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:=? \\ $$$$\:\mathrm{Y}=\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)}\:\mathrm{dx} \\ $$$$\:\mathrm{Y}=\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx} \\ $$$$\:\mathrm{Y}=\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)}\:\mathrm{dx} \\ $$$$\:\mathrm{Y}=\:\int\frac{\mathrm{d}\left(\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{2}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\:\mathrm{Y}=\:\int\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} \left(\mathrm{2}+\mathrm{y}^{\mathrm{2}} \right)}\:;\:\left[\:\mathrm{y}=\mathrm{tan}\:\mathrm{x}\:\right] \\ $$$$\:\mathrm{Y}=\int\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}+\mathrm{y}^{\mathrm{2}} }\right)\mathrm{dy} \\ $$$$\:\mathrm{Y}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{y}^{−\mathrm{2}} −\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\right)\mathrm{dy} \\ $$$$\:\mathrm{Y}=−\frac{\mathrm{1}}{\mathrm{2y}}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\:\left(\frac{\mathrm{y}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{c} \\ $$$$\:\mathrm{Y}=−\frac{\mathrm{1}}{\mathrm{2tan}\:\mathrm{x}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{arctan}\:\left(\frac{\mathrm{tan}\:\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)+\:\mathrm{c}\: \\ $$
Commented by peter frank last updated on 19/Feb/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
