Question Number 103846 by Dwaipayan Shikari last updated on 17/Jul/20

$$\int\frac{{dx}}{{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Jul/20
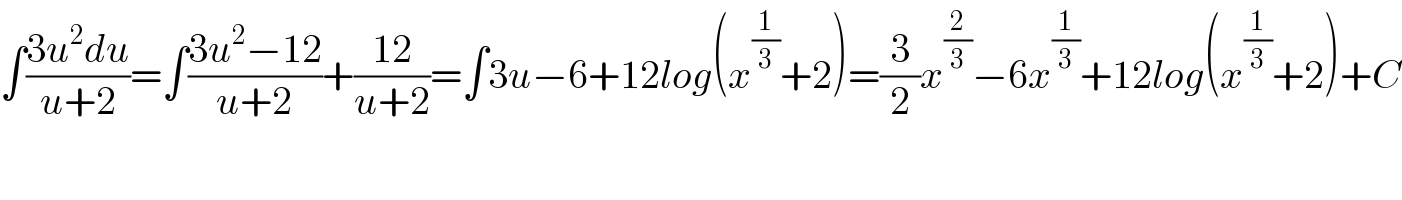
$$\int\frac{\mathrm{3}{u}^{\mathrm{2}} {du}}{{u}+\mathrm{2}}=\int\frac{\mathrm{3}{u}^{\mathrm{2}} −\mathrm{12}}{{u}+\mathrm{2}}+\frac{\mathrm{12}}{{u}+\mathrm{2}}=\int\mathrm{3}{u}−\mathrm{6}+\mathrm{12}{log}\left({x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{2}\right)=\frac{\mathrm{3}}{\mathrm{2}}{x}^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{6}{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{12}{log}\left({x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{2}\right)+{C} \\ $$
Commented by PRITHWISH SEN 2 last updated on 17/Jul/20
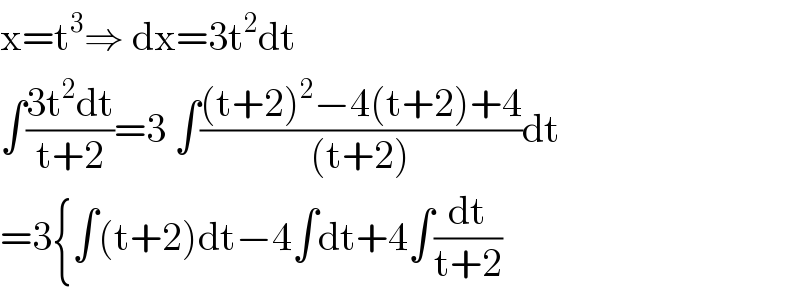
$$\mathrm{x}=\mathrm{t}^{\mathrm{3}} \Rightarrow\:\mathrm{dx}=\mathrm{3t}^{\mathrm{2}} \mathrm{dt} \\ $$$$\int\frac{\mathrm{3t}^{\mathrm{2}} \mathrm{dt}}{\mathrm{t}+\mathrm{2}}=\mathrm{3}\:\int\frac{\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{t}+\mathrm{2}\right)+\mathrm{4}}{\left(\mathrm{t}+\mathrm{2}\right)}\mathrm{dt} \\ $$$$=\mathrm{3}\left\{\int\left(\mathrm{t}+\mathrm{2}\right)\mathrm{dt}−\mathrm{4}\int\mathrm{dt}+\mathrm{4}\int\frac{\mathrm{dt}}{\mathrm{t}+\mathrm{2}}\right. \\ $$
