Question Number 124624 by bemath last updated on 04/Dec/20

$$\:\int\:\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}}\:+\mathrm{4}{x}} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Dec/20
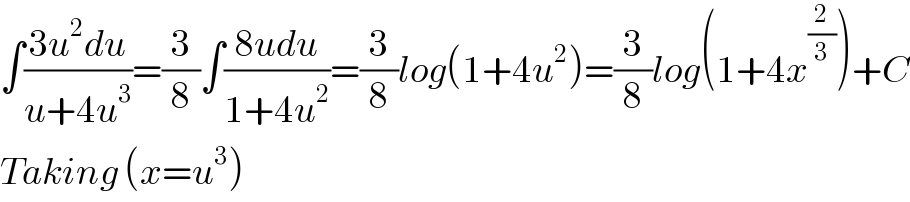
$$\int\frac{\mathrm{3}{u}^{\mathrm{2}} {du}}{{u}+\mathrm{4}{u}^{\mathrm{3}} }=\frac{\mathrm{3}}{\mathrm{8}}\int\frac{\mathrm{8}{udu}}{\mathrm{1}+\mathrm{4}{u}^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{8}}{log}\left(\mathrm{1}+\mathrm{4}{u}^{\mathrm{2}} \right)=\frac{\mathrm{3}}{\mathrm{8}}{log}\left(\mathrm{1}+\mathrm{4}{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)+{C} \\ $$$${Taking}\:\left({x}={u}^{\mathrm{3}} \right) \\ $$
