Question Number 184112 by cortano1 last updated on 03/Jan/23

$$\:\:\int\:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{5}/\mathrm{6}} \left({x}+\mathrm{2}\right)^{\mathrm{7}/\mathrm{6}} }\:=? \\ $$
Commented by sahalu last updated on 03/Jan/23
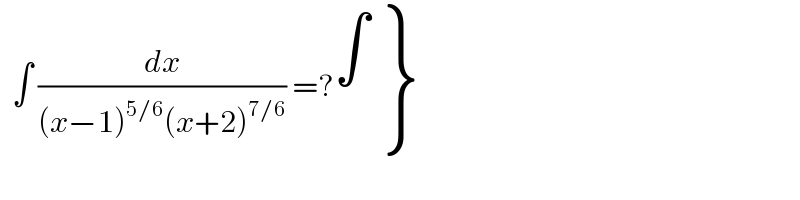
$$\:\:\int\:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{5}/\mathrm{6}} \left({x}+\mathrm{2}\right)^{\mathrm{7}/\mathrm{6}} }\:=?\left.\begin{matrix}{\int}\\{}\end{matrix}\right\} \\ $$
Answered by Frix last updated on 03/Jan/23
![∫(dx/((x−1)^(5/6) (x+2)^(7/6) ))=^( [t=(((x−1)/(x+2)))^(1/6) ] ) =2∫dt=2t=2(((x−1)/(x+2)))^(1/6) +C](https://www.tinkutara.com/question/Q184117.png)
$$\int\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{6}}} \left({x}+\mathrm{2}\right)^{\frac{\mathrm{7}}{\mathrm{6}}} }\overset{\:\:\:\:\:\left[{t}=\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} \right]\:\:\:\:\:} {=} \\ $$$$=\mathrm{2}\int{dt}=\mathrm{2}{t}=\mathrm{2}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} +{C} \\ $$
