Menu Close

dx-x-1-x-

Tinku Tara 0 Comments
Pin




Question Number 116391 by bobhans last updated on 03/Oct/20
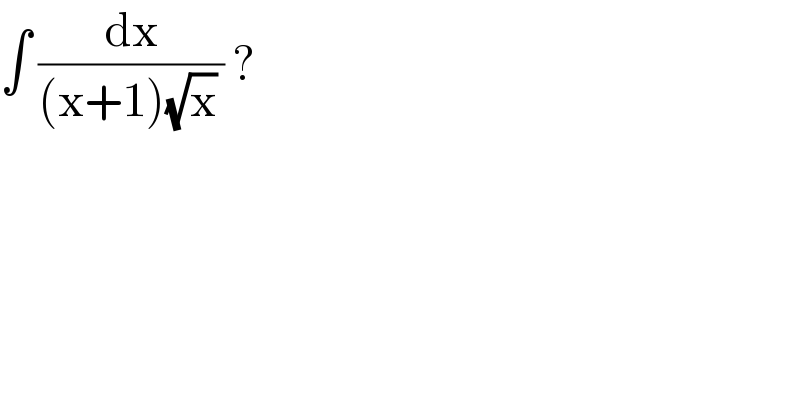
∫ (dx/((x+1)(√x) )) ?
$$\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}}\:}\:? \\ $$
Commented by TANMAY PANACEA last updated on 03/Oct/20
how to post question... here i am sharing intregation...Tanmay ∫((sinθ)/(cos3θ))+((sin3θ)/(cos9θ))+((sin9θ)/(cos27θ)) dθ
$${how}\:{to}\:{post}\:{question}… \\ $$$${here}\:{i}\:{am}\:{sharing}\:{intregation}…{Tanmay} \\ $$$$\int\frac{{sin}\theta}{{cos}\mathrm{3}\theta}+\frac{{sin}\mathrm{3}\theta}{{cos}\mathrm{9}\theta}+\frac{{sin}\mathrm{9}\theta}{{cos}\mathrm{27}\theta}\:{d}\theta \\ $$
Commented by Dwaipayan Shikari last updated on 03/Oct/20
Tap + to post question
$$\mathrm{Tap}\:+\:\mathrm{to}\:\mathrm{post}\:\mathrm{question} \\ $$
Commented by TANMAY PANACEA last updated on 03/Oct/20
ok thank you sir
$${ok}\:{thank}\:{you}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 03/Oct/20
∫((sinθ)/(4cos^3 θ−3cosθ))+∫((sin3θ)/(4cos^3 3θ−3cos3θ))+∫((sin9θ)/(4cos^3 9θ−3cos9θ)) =∫((−dt)/(4t^3 −3t))−(1/3)∫(du/(4u^3 −3u))−(1/9)∫(dp/(4p^3 −3p)) ⇒∫((−dt)/(t(4t^2 −3)))=(1/3)∫(1/t)−((4t)/(4t^2 −3))=(1/3)log(t)−(1/6)log(4t^2 −3) And similarly −(1/3)∫(du/(4u^3 −3u))=(1/9)log(u)−(1/(18))log(4u^2 −3) −(1/3)∫(dp/(4p^3 −3p))=(1/(27))log(p)−(1/(54))log(4p^2 −3) Integral is (1/3)(log(cosθ.cos^(1/3) θ.cos^(1/9) 9θ))−(1/6)(log((4cos^2 θ−3)(4cos^2 3θ−3)^(1/3) (4cos^2 9θ−3)^(1/9) )+C
$$\int\frac{\mathrm{sin}\theta}{\mathrm{4cos}^{\mathrm{3}} \theta−\mathrm{3cos}\theta}+\int\frac{\mathrm{sin3}\theta}{\mathrm{4cos}^{\mathrm{3}} \mathrm{3}\theta−\mathrm{3cos3}\theta}+\int\frac{\mathrm{sin9}\theta}{\mathrm{4cos}^{\mathrm{3}} \mathrm{9}\theta−\mathrm{3cos9}\theta} \\ $$$$=\int\frac{−\mathrm{dt}}{\mathrm{4t}^{\mathrm{3}} −\mathrm{3t}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{du}}{\mathrm{4u}^{\mathrm{3}} −\mathrm{3u}}−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\mathrm{dp}}{\mathrm{4p}^{\mathrm{3}} −\mathrm{3p}} \\ $$$$\Rightarrow\int\frac{−\mathrm{dt}}{\mathrm{t}\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{3}\right)}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{4t}}{\mathrm{4t}^{\mathrm{2}} −\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\left(\mathrm{t}\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{log}\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$\mathrm{And}\:\mathrm{similarly} \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{du}}{\mathrm{4u}^{\mathrm{3}} −\mathrm{3u}}=\frac{\mathrm{1}}{\mathrm{9}}\mathrm{log}\left(\mathrm{u}\right)−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{log}\left(\mathrm{4u}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{dp}}{\mathrm{4p}^{\mathrm{3}} −\mathrm{3p}}=\frac{\mathrm{1}}{\mathrm{27}}\mathrm{log}\left(\mathrm{p}\right)−\frac{\mathrm{1}}{\mathrm{54}}\mathrm{log}\left(\mathrm{4p}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$\mathrm{Integral}\:\mathrm{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{log}\left(\mathrm{cos}\theta.\mathrm{cos}^{\frac{\mathrm{1}}{\mathrm{3}}} \theta.\mathrm{cos}^{\frac{\mathrm{1}}{\mathrm{9}}} \mathrm{9}\theta\right)\right)−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{log}\left(\left(\mathrm{4cos}^{\mathrm{2}} \theta−\mathrm{3}\right)\left(\mathrm{4cos}^{\mathrm{2}} \mathrm{3}\theta−\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{4cos}^{\mathrm{2}} \mathrm{9}\theta−\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{9}}} \right)+\mathrm{C}\right. \\ $$
Commented by Dwaipayan Shikari last updated on 03/Oct/20
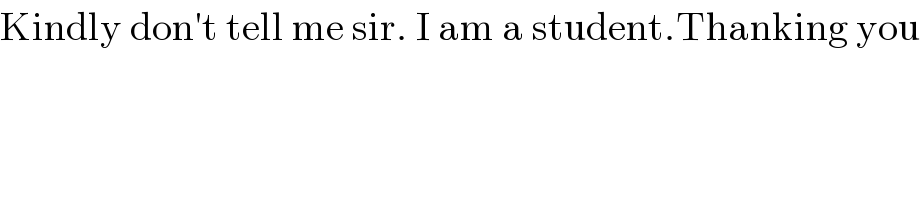
Kindly don′t tell me sir. I am a student.Thanking you
$$\mathrm{Kindly}\:\mathrm{don}'\mathrm{t}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{a}\:\mathrm{student}.\mathrm{Thanking}\:\mathrm{you} \\ $$
Commented by mnjuly1970 last updated on 03/Oct/20
good for you nice solution peace be upon you...
$$\:\:{good}\:{for}\:\:{you}\:\:{nice}\:{solution} \\ $$$${peace}\:\:{be}\:{upon}\:{you}… \\ $$
Commented by TANMAY PANACEA last updated on 03/Oct/20
tan3θ−tanθ =((sin3θcosθ−sinθcos3θ)/(cos3θcosθ))=((2sinθcosθ)/(cos3θcosθ)) ((sinθ)/(cos3θ))=(1/2)[tan3θ−tanθ] ((sin3θ)/(cos9θ))=(1/2)[tan9θ−tan3θ] ((sin9θ)/(cos27θ))=(1/2)[tan27θ−tan9θ] add them=(1/2)[tan27θ−tanθ] so I=∫(1/2)(tan27θ−tanθ)dθ =(1/2)[((lnsec27θ)/(27))−lnsecθ]+c
$${tan}\mathrm{3}\theta−{tan}\theta \\ $$$$=\frac{{sin}\mathrm{3}\theta{cos}\theta−{sin}\theta{cos}\mathrm{3}\theta}{{cos}\mathrm{3}\theta{cos}\theta}=\frac{\mathrm{2}{sin}\theta{cos}\theta}{{cos}\mathrm{3}\theta{cos}\theta} \\ $$$$\frac{{sin}\theta}{{cos}\mathrm{3}\theta}=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}\mathrm{3}\theta−{tan}\theta\right] \\ $$$$\frac{{sin}\mathrm{3}\theta}{{cos}\mathrm{9}\theta}=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}\mathrm{9}\theta−{tan}\mathrm{3}\theta\right] \\ $$$$\frac{{sin}\mathrm{9}\theta}{{cos}\mathrm{27}\theta}=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}\mathrm{27}\theta−{tan}\mathrm{9}\theta\right] \\ $$$${add}\:{them}=\frac{\mathrm{1}}{\mathrm{2}}\left[{tan}\mathrm{27}\theta−{tan}\theta\right] \\ $$$${so}\:{I}=\int\frac{\mathrm{1}}{\mathrm{2}}\left({tan}\mathrm{27}\theta−{tan}\theta\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{lnsec}\mathrm{27}\theta}{\mathrm{27}}−{lnsec}\theta\right]+{c} \\ $$$$ \\ $$
Answered by bemath last updated on 03/Oct/20
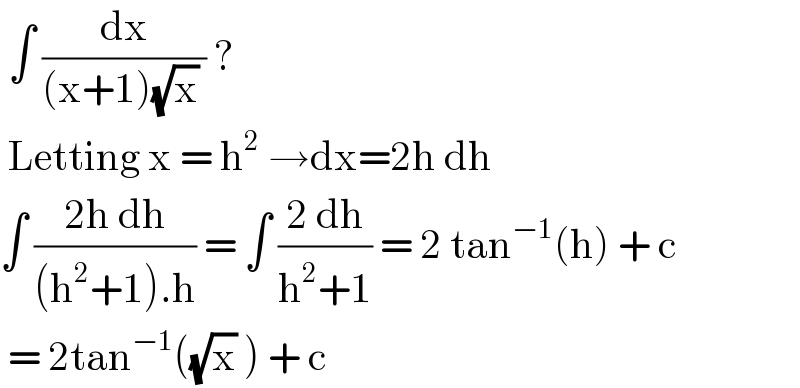
∫ (dx/((x+1)(√x) )) ? Letting x = h^2 →dx=2h dh ∫ ((2h dh)/((h^2 +1).h)) = ∫ ((2 dh)/(h^2 +1)) = 2 tan^(−1) (h) + c = 2tan^(−1) ((√x) ) + c
$$\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}}\:}\:? \\ $$$$\:\mathrm{Letting}\:\mathrm{x}\:=\:\mathrm{h}^{\mathrm{2}} \:\rightarrow\mathrm{dx}=\mathrm{2h}\:\mathrm{dh} \\ $$$$\int\:\frac{\mathrm{2h}\:\mathrm{dh}}{\left(\mathrm{h}^{\mathrm{2}} +\mathrm{1}\right).\mathrm{h}}\:=\:\int\:\frac{\mathrm{2}\:\mathrm{dh}}{\mathrm{h}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{h}\right)\:+\:\mathrm{c} \\ $$$$\:=\:\mathrm{2tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\:\right)\:+\:\mathrm{c}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *