Question Number 20254 by tammi last updated on 24/Aug/17
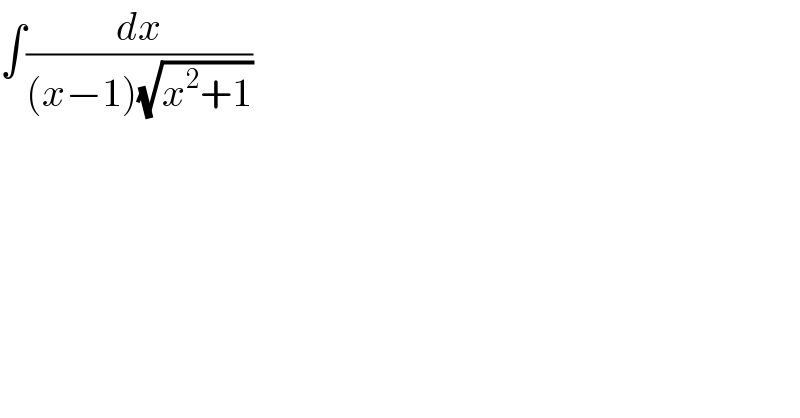
$$\int\frac{{dx}}{\left({x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$
Answered by $@ty@m last updated on 25/Aug/17

$${Let}\:{x}−\mathrm{1}=\frac{\mathrm{1}}{{t}} \\ $$$$\Rightarrow{dx}=\frac{−\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\therefore\:{I}=\int\frac{\frac{−\mathrm{1}}{{t}^{\mathrm{2}} }{dt}}{\frac{\mathrm{1}}{{t}}\sqrt{\left(\frac{\mathrm{1}}{{t}}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}} \\ $$$$=\int\frac{−{dt}}{\:\sqrt{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} +{t}^{\mathrm{2}} }} \\ $$$$=\int\frac{−{dt}}{\:\sqrt{\mathrm{1}+\mathrm{2}{t}+\mathrm{2}{t}^{\mathrm{2}} }} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}{t}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}}} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dt}}{\:\sqrt{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}.{ln}\mid\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\mid+{C}\:,\:{where}\:{t}=\frac{\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by tammi last updated on 25/Aug/17

$${thank}\:{u} \\ $$
