dx-x-1-x-2-2-

Question Number 94143 by john santu last updated on 17/May/20

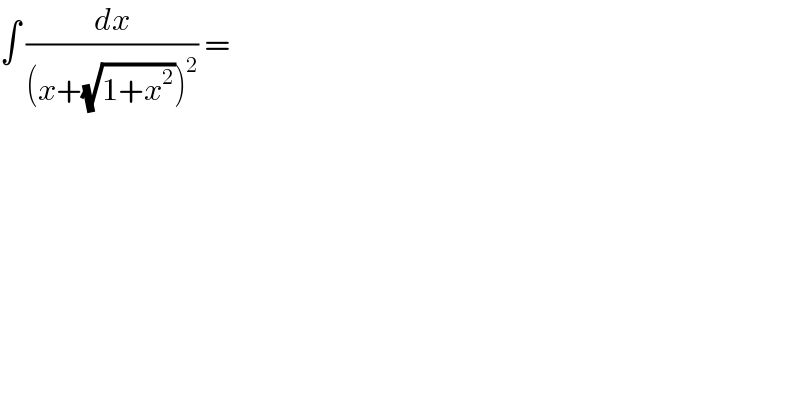
$$\int\:\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:= \\ $$

Commented by abdomathmax last updated on 17/May/20

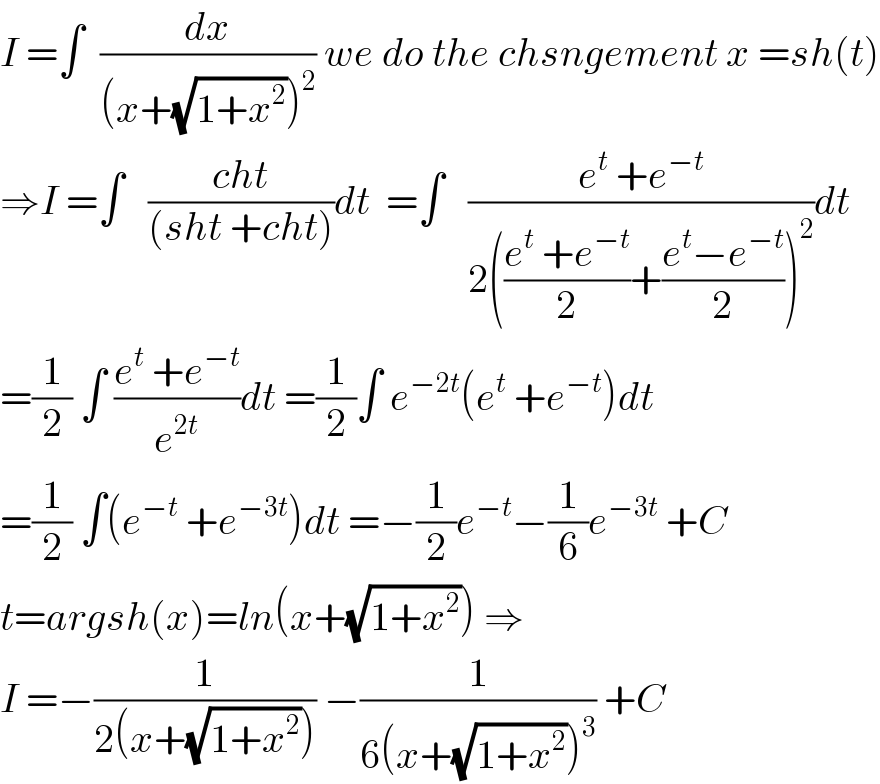
I =∫ (dx/((x+(√(1+x^2 )))^2 )) we do the chsngement x =sh(t) ⇒I =∫ ((cht)/((sht +cht)))dt =∫ ((e^t +e^(−t) )/(2(((e^t +e^(−t) )/2)+((e^t −e^(−t) )/2))^2 ))dt =(1/2) ∫ ((e^t +e^(−t) )/e^(2t) )dt =(1/2)∫ e^(−2t) (e^t +e^(−t) )dt =(1/2) ∫(e^(−t) +e^(−3t) )dt =−(1/2)e^(−t) −(1/6)e^(−3t) +C t=argsh(x)=ln(x+(√(1+x^2 ))) ⇒ I =−(1/(2(x+(√(1+x^2 ))))) −(1/(6(x+(√(1+x^2 )))^3 )) +C

$${I}\:=\int\:\:\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{we}\:{do}\:{the}\:{chsngement}\:{x}\:={sh}\left({t}\right) \\ $$$$\Rightarrow{I}\:=\int\:\:\:\frac{{cht}}{\left({sht}\:+{cht}\right)}{dt}\:\:=\int\:\:\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}\left(\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}+\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{{e}^{\mathrm{2}{t}} }{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:{e}^{−\mathrm{2}{t}} \left({e}^{{t}} \:+{e}^{−{t}} \right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\left({e}^{−{t}} \:+{e}^{−\mathrm{3}{t}} \right){dt}\:=−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{t}} −\frac{\mathrm{1}}{\mathrm{6}}{e}^{−\mathrm{3}{t}} \:+{C} \\ $$$${t}={argsh}\left({x}\right)={ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)}\:−\frac{\mathrm{1}}{\mathrm{6}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{3}} }\:+{C} \\ $$

Commented by i jagooll last updated on 17/May/20

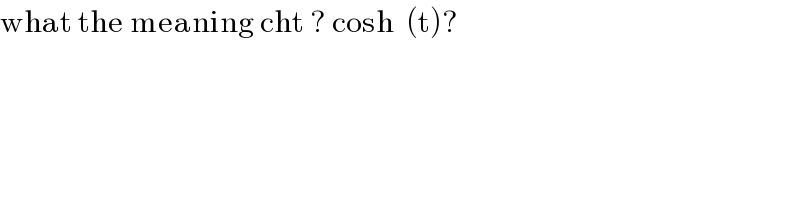
$$\mathrm{what}\:\mathrm{the}\:\mathrm{meaning}\:\mathrm{cht}\:?\:\mathrm{cosh}\:\:\left(\mathrm{t}\right)? \\ $$

Commented by mathmax by abdo last updated on 17/May/20

cht =((e^t +e^(−t) )/2) (→hyperbolic cos) sh(t) =((e^t −e^(−t) )/2)(→hyperbolic sin)

$${cht}\:=\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}\:\left(\rightarrow{hyperbolic}\:{cos}\right) \\ $$$${sh}\left({t}\right)\:=\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}\left(\rightarrow{hyperbolic}\:{sin}\right) \\ $$

Answered by john santu last updated on 17/May/20

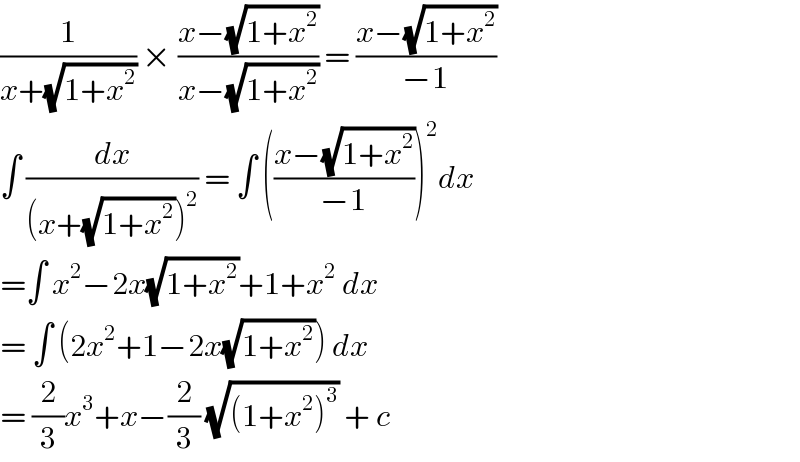
(1/(x+(√(1+x^2 )))) × ((x−(√(1+x^2 )))/(x−(√(1+x^2 )))) = ((x−(√(1+x^2 )))/(−1)) ∫ (dx/((x+(√(1+x^2 )))^2 )) = ∫ (((x−(√(1+x^2 )))/(−1)))^2 dx =∫ x^2 −2x(√(1+x^2 ))+1+x^2 dx = ∫ (2x^2 +1−2x(√(1+x^2 ))) dx = (2/3)x^3 +x−(2/3) (√((1+x^2 )^3 )) + c

$$\frac{\mathrm{1}}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:×\:\frac{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:=\:\frac{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{−\mathrm{1}} \\ $$$$\int\:\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:=\:\int\:\left(\frac{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{−\mathrm{1}}\right)^{\mathrm{2}} {dx} \\ $$$$=\int\:{x}^{\mathrm{2}} −\mathrm{2}{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}+{x}^{\mathrm{2}} \:{dx} \\ $$$$=\:\int\:\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:{dx}\: \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} +{x}−\frac{\mathrm{2}}{\mathrm{3}}\:\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:+\:{c}\: \\ $$

Commented by i jagooll last updated on 17/May/20

cool man ��

Facebook Tweet Pin

Leave a Reply Cancel reply