Menu Close

dx-x-2-1-x-2-4-

Tinku Tara 0 Comments
Pin




Question Number 86302 by john santu last updated on 28/Mar/20
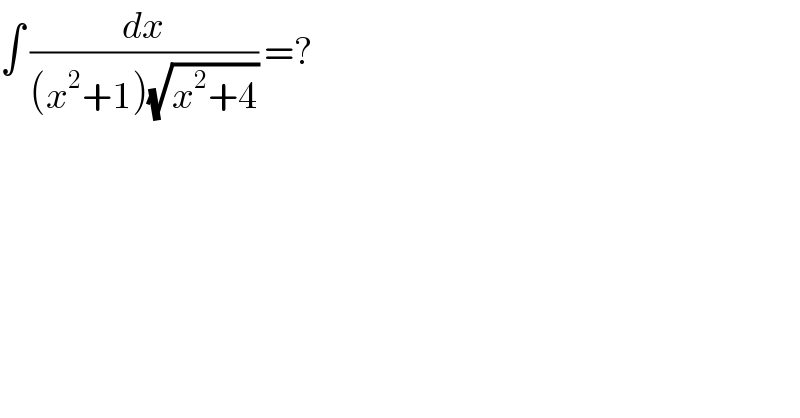
∫ (dx/((x^2 +1)(√(x^2 +4)))) =?
$$\int\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}\:=? \\ $$
Commented by abdomathmax last updated on 28/Mar/20
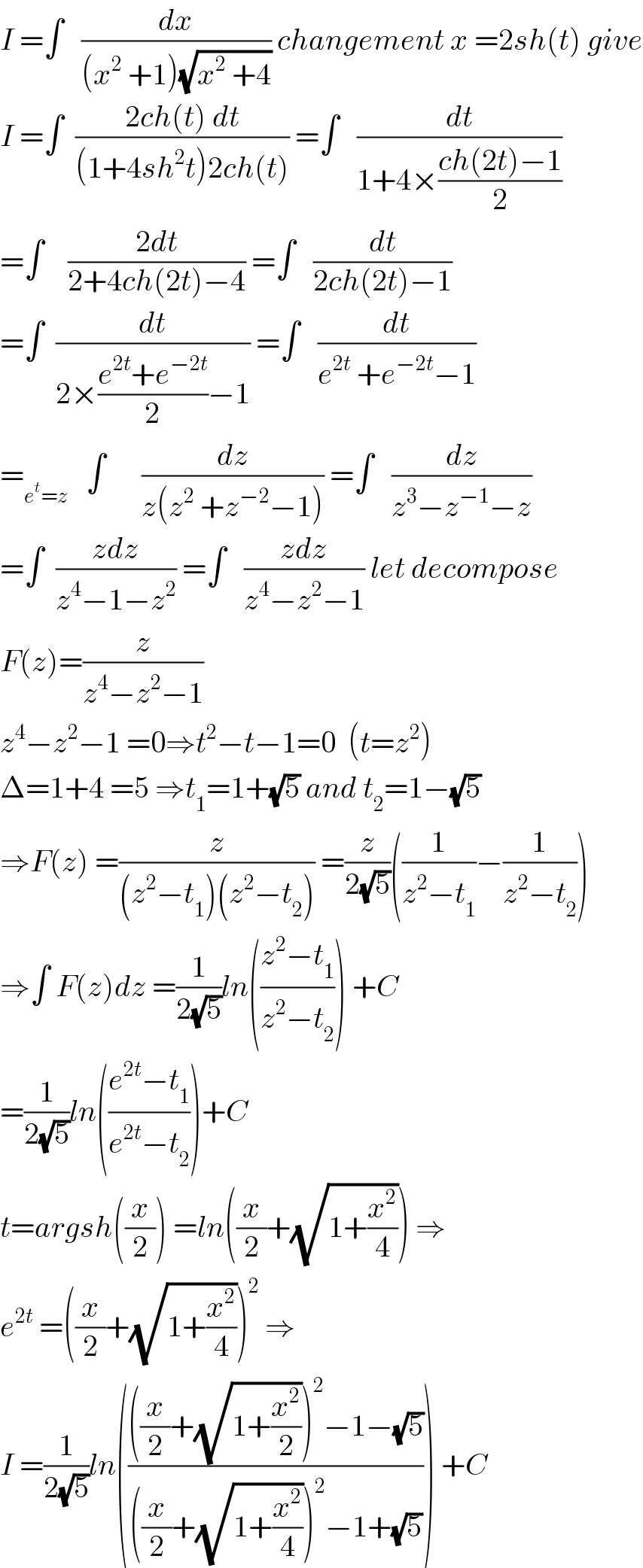
I =∫ (dx/((x^2 +1)(√(x^2 +4)))) changement x =2sh(t) give I =∫ ((2ch(t) dt)/((1+4sh^2 t)2ch(t))) =∫ (dt/(1+4×((ch(2t)−1)/2))) =∫ ((2dt)/(2+4ch(2t)−4)) =∫ (dt/(2ch(2t)−1)) =∫ (dt/(2×((e^(2t) +e^(−2t) )/2)−1)) =∫ (dt/(e^(2t) +e^(−2t) −1)) =_(e^t =z) ∫ (dz/(z(z^2 +z^(−2) −1))) =∫ (dz/(z^3 −z^(−1) −z)) =∫ ((zdz)/(z^4 −1−z^2 )) =∫ ((zdz)/(z^4 −z^2 −1)) let decompose F(z)=(z/(z^4 −z^2 −1)) z^4 −z^2 −1 =0⇒t^2 −t−1=0 (t=z^2 ) Δ=1+4 =5 ⇒t_1 =1+(√5) and t_2 =1−(√5) ⇒F(z) =(z/((z^2 −t_1 )(z^2 −t_2 ))) =(z/(2(√5)))((1/(z^2 −t_1 ))−(1/(z^2 −t_2 ))) ⇒∫ F(z)dz =(1/(2(√5)))ln(((z^2 −t_1 )/(z^2 −t_2 ))) +C =(1/(2(√5)))ln(((e^(2t) −t_1 )/(e^(2t) −t_2 )))+C t=argsh((x/2)) =ln((x/2)+(√(1+(x^2 /4)))) ⇒ e^(2t) =((x/2)+(√(1+(x^2 /4))))^2 ⇒ I =(1/(2(√5)))ln(((((x/2)+(√(1+(x^2 /2))))^2 −1−(√5))/(((x/2)+(√(1+(x^2 /4))))^2 −1+(√5)))) +C
$${I}\:=\int\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}}}\:{changement}\:{x}\:=\mathrm{2}{sh}\left({t}\right)\:{give} \\ $$$${I}\:=\int\:\:\frac{\mathrm{2}{ch}\left({t}\right)\:{dt}}{\left(\mathrm{1}+\mathrm{4}{sh}^{\mathrm{2}} {t}\right)\mathrm{2}{ch}\left({t}\right)}\:=\int\:\:\:\frac{{dt}}{\mathrm{1}+\mathrm{4}×\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\int\:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}+\mathrm{4}{ch}\left(\mathrm{2}{t}\right)−\mathrm{4}}\:=\int\:\:\:\frac{{dt}}{\mathrm{2}{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}} \\ $$$$=\int\:\:\frac{{dt}}{\mathrm{2}×\frac{{e}^{\mathrm{2}{t}} +{e}^{−\mathrm{2}{t}} }{\mathrm{2}}−\mathrm{1}}\:=\int\:\:\:\frac{{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} −\mathrm{1}} \\ $$$$=_{{e}^{{t}} ={z}} \:\:\:\int\:\:\:\:\:\:\frac{{dz}}{{z}\left({z}^{\mathrm{2}} \:+{z}^{−\mathrm{2}} −\mathrm{1}\right)}\:=\int\:\:\:\frac{{dz}}{{z}^{\mathrm{3}} −{z}^{−\mathrm{1}} −{z}} \\ $$$$=\int\:\:\frac{{zdz}}{{z}^{\mathrm{4}} −\mathrm{1}−{z}^{\mathrm{2}} }\:=\int\:\:\:\frac{{zdz}}{{z}^{\mathrm{4}} −{z}^{\mathrm{2}} −\mathrm{1}}\:{let}\:{decompose} \\ $$$${F}\left({z}\right)=\frac{{z}}{{z}^{\mathrm{4}} −{z}^{\mathrm{2}} −\mathrm{1}} \\ $$$${z}^{\mathrm{4}} −{z}^{\mathrm{2}} −\mathrm{1}\:=\mathrm{0}\Rightarrow{t}^{\mathrm{2}} −{t}−\mathrm{1}=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=\mathrm{1}+\mathrm{4}\:=\mathrm{5}\:\Rightarrow{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{5}}\:{and}\:{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{F}\left({z}\right)\:=\frac{{z}}{\left({z}^{\mathrm{2}} −{t}_{\mathrm{1}} \right)\left({z}^{\mathrm{2}} −{t}_{\mathrm{2}} \right)}\:=\frac{{z}}{\mathrm{2}\sqrt{\mathrm{5}}}\left(\frac{\mathrm{1}}{{z}^{\mathrm{2}} −{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{{z}^{\mathrm{2}} −{t}_{\mathrm{2}} }\right) \\ $$$$\Rightarrow\int\:{F}\left({z}\right){dz}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}{ln}\left(\frac{{z}^{\mathrm{2}} −{t}_{\mathrm{1}} }{{z}^{\mathrm{2}} −{t}_{\mathrm{2}} }\right)\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}{ln}\left(\frac{{e}^{\mathrm{2}{t}} −{t}_{\mathrm{1}} }{{e}^{\mathrm{2}{t}} −{t}_{\mathrm{2}} }\right)+{C} \\ $$$${t}={argsh}\left(\frac{{x}}{\mathrm{2}}\right)\:={ln}\left(\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\right)\:\Rightarrow \\ $$$${e}^{\mathrm{2}{t}} \:=\left(\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}{ln}\left(\frac{\left(\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{1}−\sqrt{\mathrm{5}}}{\left(\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\right)^{\mathrm{2}} −\mathrm{1}+\sqrt{\mathrm{5}}}\right)\:+{C} \\ $$
Answered by TANMAY PANACEA. last updated on 28/Mar/20
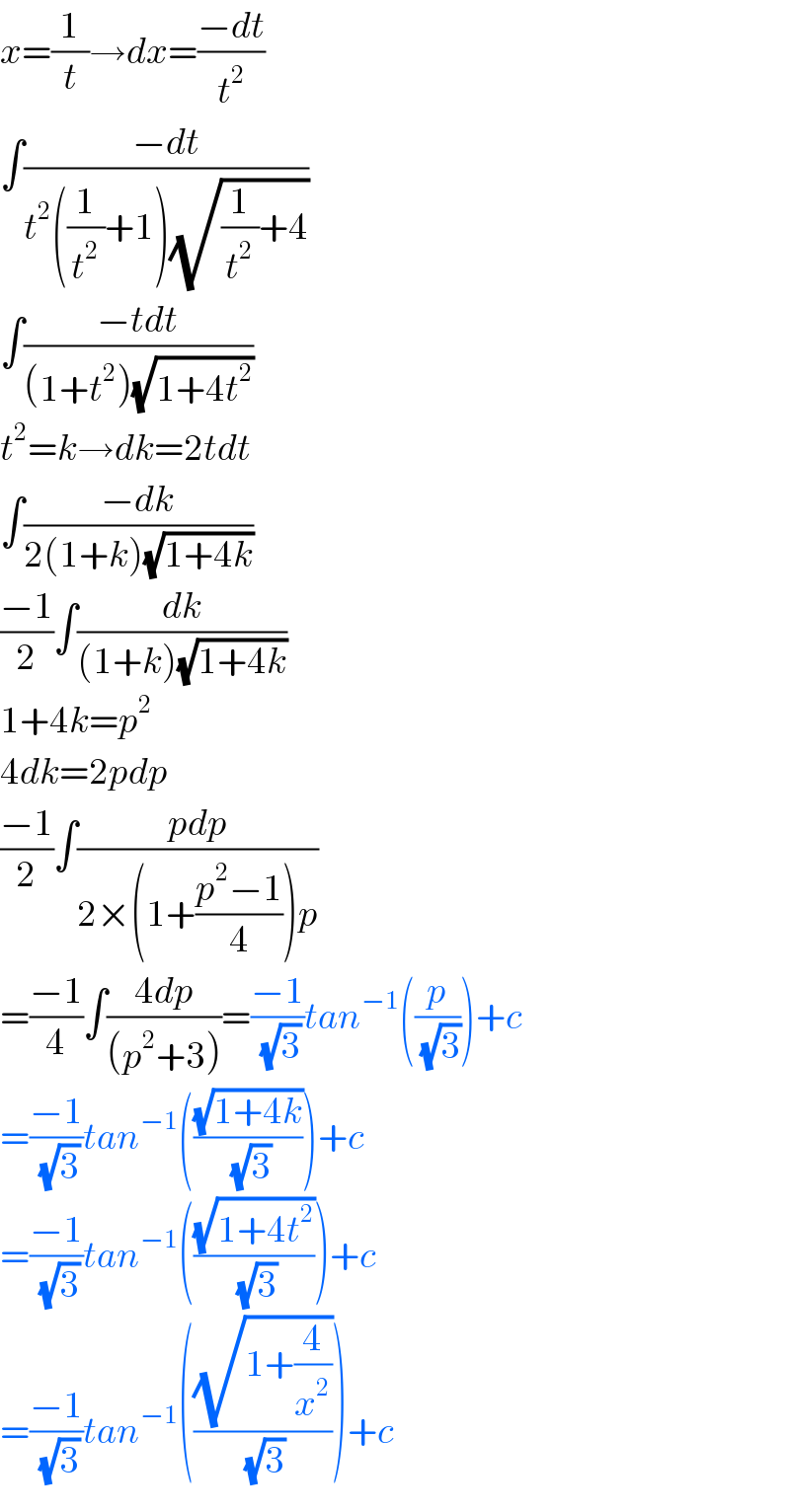
x=(1/t)→dx=((−dt)/t^2 ) ∫((−dt)/(t^2 ((1/t^2 )+1)(√((1/t^2 )+4)))) ∫((−tdt)/((1+t^2 )(√(1+4t^2 )))) t^2 =k→dk=2tdt ∫((−dk)/(2(1+k)(√(1+4k)))) ((−1)/2)∫(dk/((1+k)(√(1+4k)))) 1+4k=p^2 4dk=2pdp ((−1)/2)∫((pdp)/(2×(1+((p^2 −1)/4))p)) =((−1)/4)∫((4dp)/((p^2 +3)))=((−1)/( (√3)))tan^(−1) ((p/( (√3))))+c =((−1)/( (√3)))tan^(−1) (((√(1+4k))/( (√3))))+c =((−1)/( (√3)))tan^(−1) (((√(1+4t^2 ))/( (√3))))+c =((−1)/( (√3)))tan^(−1) (((√(1+(4/x^2 )))/( (√3))))+c
$${x}=\frac{\mathrm{1}}{{t}}\rightarrow{dx}=\frac{−{dt}}{{t}^{\mathrm{2}} } \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{1}\right)\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{4}}} \\ $$$$\int\frac{−{tdt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }} \\ $$$${t}^{\mathrm{2}} ={k}\rightarrow{dk}=\mathrm{2}{tdt} \\ $$$$\int\frac{−{dk}}{\mathrm{2}\left(\mathrm{1}+{k}\right)\sqrt{\mathrm{1}+\mathrm{4}{k}}} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{dk}}{\left(\mathrm{1}+{k}\right)\sqrt{\mathrm{1}+\mathrm{4}{k}}} \\ $$$$\mathrm{1}+\mathrm{4}{k}={p}^{\mathrm{2}} \\ $$$$\mathrm{4}{dk}=\mathrm{2}{pdp} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{pdp}}{\mathrm{2}×\left(\mathrm{1}+\frac{{p}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}\right){p}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}{dp}}{\left({p}^{\mathrm{2}} +\mathrm{3}\right)}=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{p}}{\:\sqrt{\mathrm{3}}}\right)+{c} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+\mathrm{4}{k}}}{\:\sqrt{\mathrm{3}}}\right)+{c} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{3}}}\right)+{c} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+\frac{\mathrm{4}}{{x}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{3}}}\right)+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *