Question Number 153109 by peter frank last updated on 04/Sep/21
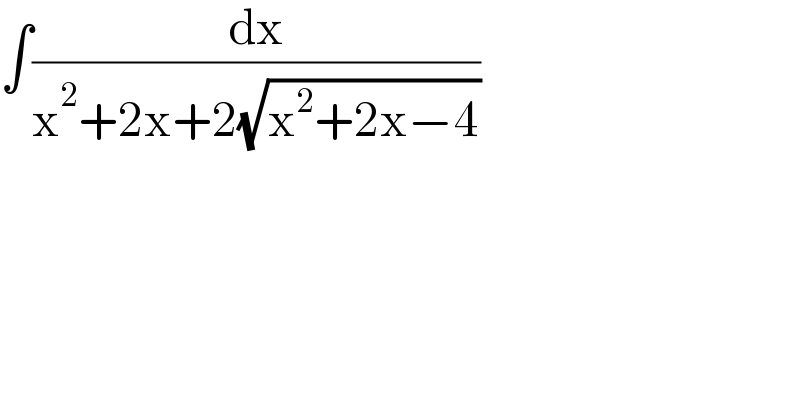
$$\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{4}}} \\ $$
Commented by MJS_new last updated on 05/Sep/21

$$\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{clear}\:\mathrm{but}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{are}\:\mathrm{weird} \\ $$$${t}=\frac{{x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{4}}}{\:\sqrt{\mathrm{5}}}\:\Leftrightarrow\:{x}=\frac{\sqrt{\mathrm{5}}{t}^{\mathrm{2}} −\mathrm{2}{t}+\sqrt{\mathrm{5}}}{\mathrm{2}{t}} \\ $$$$\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{4}}}{{t}}{dt} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}}\int\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{4}} +\frac{\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{5}}{t}^{\mathrm{3}} +\frac{\mathrm{6}}{\mathrm{5}}{t}^{\mathrm{2}} +\frac{\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{5}}{t}+\mathrm{1}}{dt} \\ $$$${u}={t}+\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\:\Leftrightarrow\:{t}={u}−\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\:\rightarrow\:{dt}={du} \\ $$$$\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}}\int\frac{{u}^{\mathrm{2}} −\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}}{u}−\frac{\mathrm{4}}{\mathrm{5}}}{{u}^{\mathrm{4}} −\frac{\mathrm{24}\sqrt{\mathrm{5}}}{\mathrm{25}}{u}+\frac{\mathrm{48}}{\mathrm{25}}}{du} \\ $$$${u}^{\mathrm{4}} −\frac{\mathrm{24}\sqrt{\mathrm{5}}}{\mathrm{25}}{u}+\frac{\mathrm{48}}{\mathrm{25}}= \\ $$$$=\left({u}^{\mathrm{2}} −\frac{\sqrt{\mathrm{10}\left(\mathrm{3}+\sqrt{\mathrm{21}}\right)}}{\mathrm{5}}{u}+\frac{\mathrm{3}+\sqrt{\mathrm{21}}−\sqrt{\mathrm{6}\left(−\mathrm{3}+\sqrt{\mathrm{21}}\right)}}{\mathrm{5}}\right)× \\ $$$$×\left({u}^{\mathrm{2}} +\frac{\sqrt{\mathrm{10}\left(\mathrm{3}+\sqrt{\mathrm{21}}\right)}}{\mathrm{5}}{u}+\frac{\mathrm{3}+\sqrt{\mathrm{21}}+\sqrt{\mathrm{6}\left(+\mathrm{3}+\sqrt{\mathrm{21}}\right)}}{\mathrm{5}}\right) \\ $$$$\mathrm{and}\:\mathrm{now}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{decompose}… \\ $$
