Question Number 127203 by naka3546 last updated on 27/Dec/20
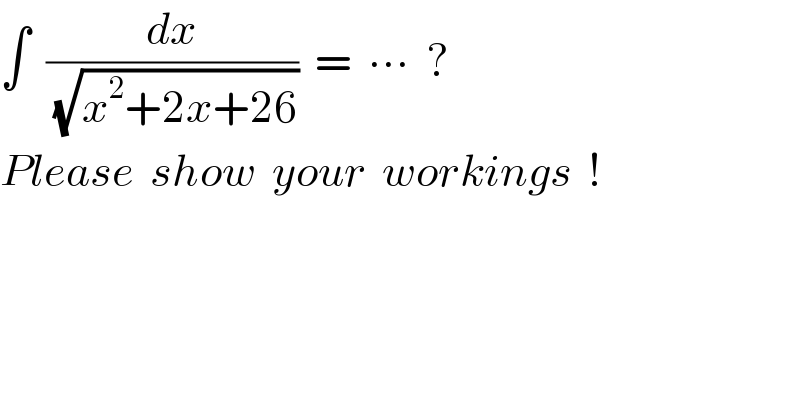
$$\int\:\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{26}}}\:\:=\:\:\centerdot\centerdot\centerdot\:\:? \\ $$$${Please}\:\:{show}\:\:{your}\:\:{workings}\:\:! \\ $$
Commented by liberty last updated on 27/Dec/20
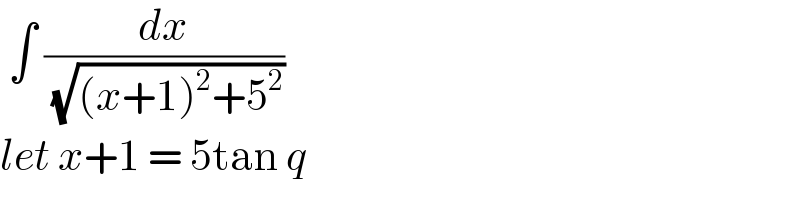
$$\:\int\:\frac{{dx}}{\:\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }}\: \\ $$$${let}\:{x}+\mathrm{1}\:=\:\mathrm{5tan}\:{q}\: \\ $$
Commented by Ar Brandon last updated on 27/Dec/20
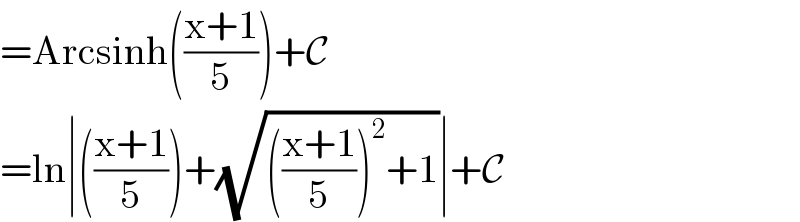
$$=\mathrm{Arcsinh}\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{5}}\right)+\mathcal{C} \\ $$$$=\mathrm{ln}\mid\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{5}}\right)+\sqrt{\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} +\mathrm{1}}\mid+\mathcal{C} \\ $$
Answered by Ar Brandon last updated on 27/Dec/20
![I=∫(dx/( (√(x^2 +2x+26)))) [t=x+1+(√(x^2 +2x+26)) ⇒ dt=(t/( (√(x^2 +2x+26))))dx] I=∫(1/t)dt=ln∣t∣+C=ln∣(x+1)+(√(x^2 +2x+26)) ∣+C](https://www.tinkutara.com/question/Q127207.png)
$$\mathcal{I}=\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{26}}} \\ $$$$\left[\mathrm{t}=\mathrm{x}+\mathrm{1}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{26}}\:\Rightarrow\:\mathrm{dt}=\frac{\mathrm{t}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{26}}}\mathrm{dx}\right] \\ $$$$\mathcal{I}=\int\frac{\mathrm{1}}{\mathrm{t}}\mathrm{dt}=\mathrm{ln}\mid\mathrm{t}\mid+\mathrm{C}=\mathrm{ln}\mid\left(\mathrm{x}+\mathrm{1}\right)+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{26}}\:\mid+\mathrm{C} \\ $$
Answered by Mr.D.N. last updated on 27/Dec/20
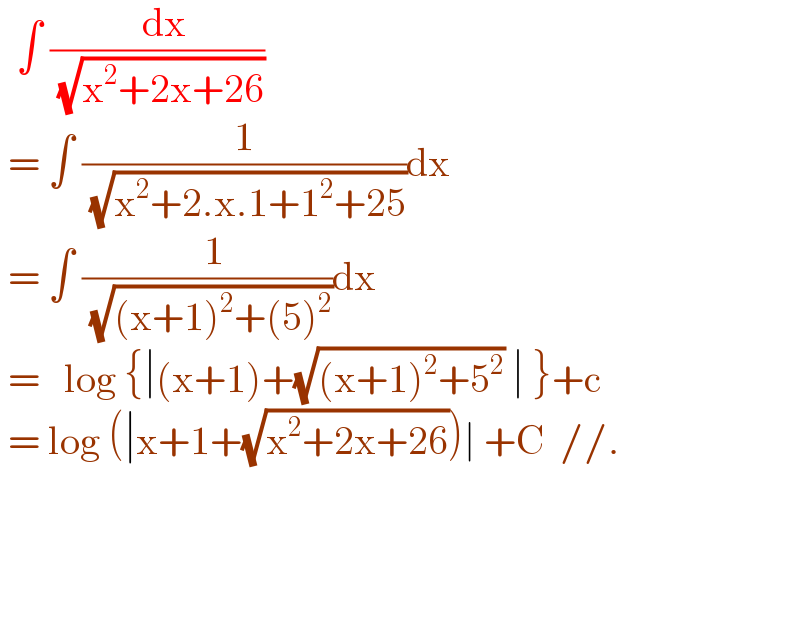
$$\:\:\int\:\frac{\:\:\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{26}}} \\ $$$$\:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2}.\mathrm{x}.\mathrm{1}+\mathrm{1}^{\mathrm{2}} +\mathrm{25}}}\mathrm{dx} \\ $$$$\:=\:\int\:\frac{\:\:\mathrm{1}}{\:\sqrt{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{5}\right)^{\mathrm{2}} }}\mathrm{dx} \\ $$$$\:=\:\:\:\mathrm{log}\:\left\{\mid\left(\mathrm{x}+\mathrm{1}\right)+\sqrt{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }\:\mid\:\right\}+\mathrm{c} \\ $$$$\:=\:\mathrm{log}\:\left(\mid\mathrm{x}+\mathrm{1}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{26}}\right)\mid\:+\mathrm{C}\:\://. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
