Question Number 167145 by mkam last updated on 07/Mar/22

$$\int\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{3}\sqrt{{x}}+\mathrm{10}} \\ $$
Commented by MJS_new last updated on 07/Mar/22
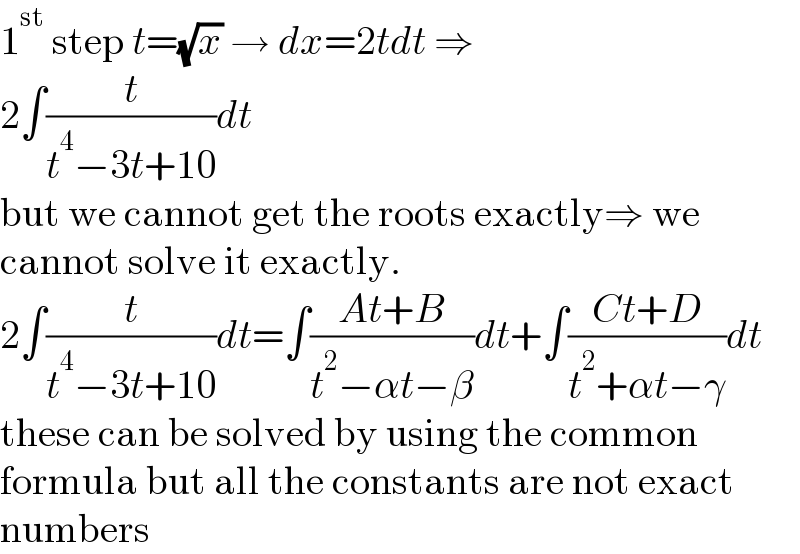
$$\mathrm{1}^{\mathrm{st}} \:\mathrm{step}\:{t}=\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}{tdt}\:\Rightarrow \\ $$$$\mathrm{2}\int\frac{{t}}{{t}^{\mathrm{4}} −\mathrm{3}{t}+\mathrm{10}}{dt} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{get}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{exactly}\Rightarrow\:\mathrm{we} \\ $$$$\mathrm{cannot}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{exactly}. \\ $$$$\mathrm{2}\int\frac{{t}}{{t}^{\mathrm{4}} −\mathrm{3}{t}+\mathrm{10}}{dt}=\int\frac{{At}+{B}}{{t}^{\mathrm{2}} −\alpha{t}−\beta}{dt}+\int\frac{{Ct}+{D}}{{t}^{\mathrm{2}} +\alpha{t}−\gamma}{dt} \\ $$$$\mathrm{these}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{by}\:\mathrm{using}\:\mathrm{the}\:\mathrm{common} \\ $$$$\mathrm{formula}\:\mathrm{but}\:\mathrm{all}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{are}\:\mathrm{not}\:\mathrm{exact} \\ $$$$\mathrm{numbers} \\ $$
