Question Number 120703 by bobhans last updated on 02/Nov/20
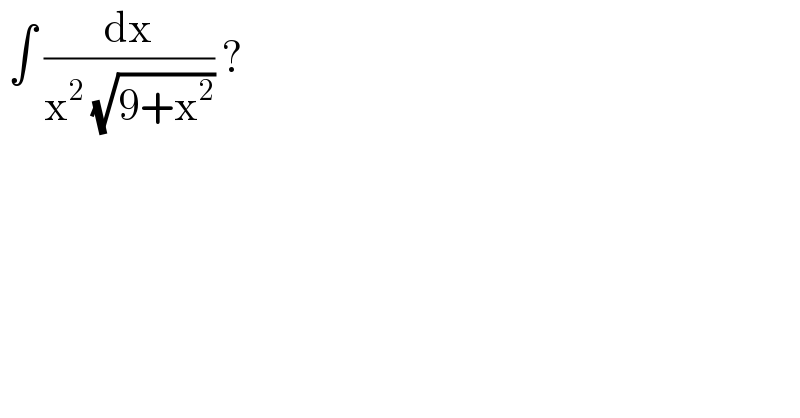
$$\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:\sqrt{\mathrm{9}+\mathrm{x}^{\mathrm{2}} }}\:? \\ $$
Answered by john santu last updated on 02/Nov/20
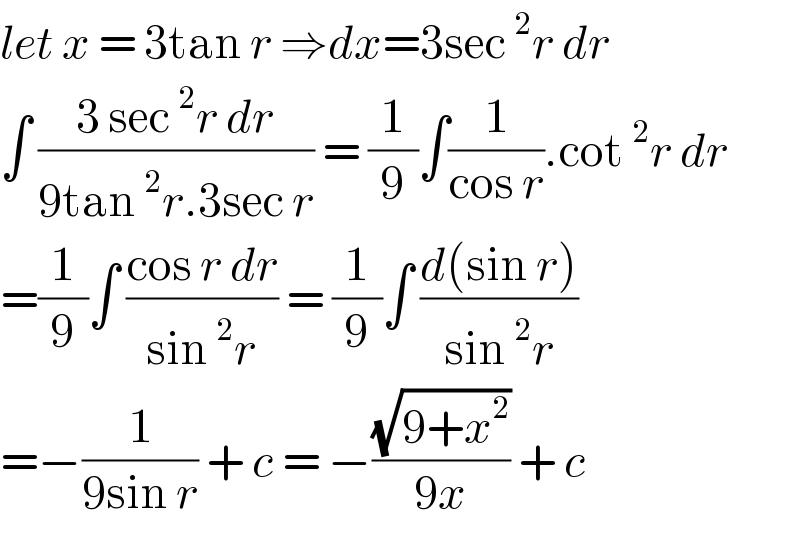
$${let}\:{x}\:=\:\mathrm{3tan}\:{r}\:\Rightarrow{dx}=\mathrm{3sec}\:^{\mathrm{2}} {r}\:{dr} \\ $$$$\int\:\frac{\mathrm{3}\:\mathrm{sec}\:^{\mathrm{2}} {r}\:{dr}}{\mathrm{9tan}\:^{\mathrm{2}} {r}.\mathrm{3sec}\:{r}}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\mathrm{1}}{\mathrm{cos}\:{r}}.\mathrm{cot}\:^{\mathrm{2}} {r}\:{dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\int\:\frac{\mathrm{cos}\:{r}\:{dr}}{\mathrm{sin}\:^{\mathrm{2}} {r}}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\int\:\frac{{d}\left(\mathrm{sin}\:{r}\right)}{\mathrm{sin}\:^{\mathrm{2}} {r}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{9sin}\:{r}}\:+\:{c}\:=\:−\frac{\sqrt{\mathrm{9}+{x}^{\mathrm{2}} }}{\mathrm{9}{x}}\:+\:{c} \\ $$
Commented by malwaan last updated on 04/Nov/20

$${yes}\:{sir} \\ $$$${you}\:{are}\:{right} \\ $$
