Question Number 156820 by tabata last updated on 15/Oct/21
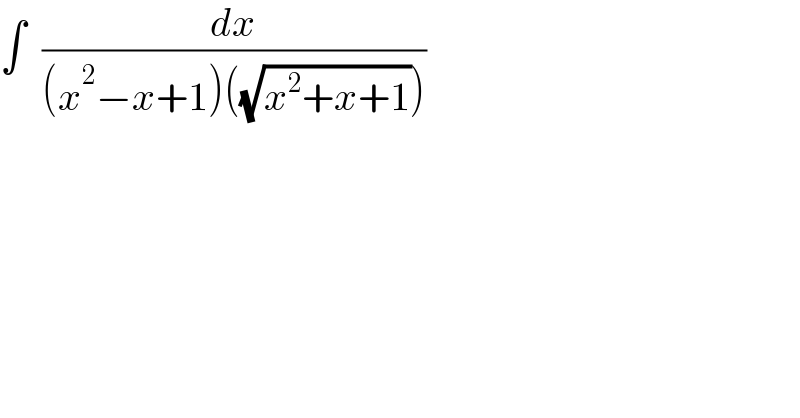
$$\int\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)} \\ $$
Commented by tabata last updated on 15/Oct/21

$$????? \\ $$
Commented by MJS_new last updated on 16/Oct/21
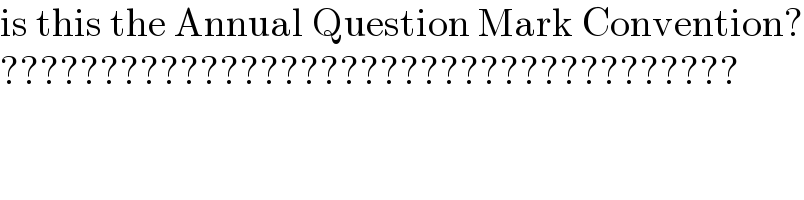
$$\mathrm{is}\:\mathrm{this}\:\mathrm{the}\:\mathrm{Annual}\:\mathrm{Question}\:\mathrm{Mark}\:\mathrm{Convention}? \\ $$$$????????????????????????????????????? \\ $$
Commented by aliyn last updated on 16/Oct/21

$$??????? \\ $$
Answered by MJS_new last updated on 16/Oct/21
![∫(dx/((x^2 −x+1)(√(x^2 +x+1))))= [t=(((√3)t^2 −2t−(√3))/(4t)) → dx=((√(3(x^2 +x+1)))/(2x+1+2(√(x^2 +x+1))))] =((16)/3)∫(t/(t^4 −((8(√3))/3)t^3 +((22)/3)t^2 +((8(√3))/3)t+1))dt= =((16)/3)∫(t/((t^2 −(2(√2)−((4(√3))/3))t+5−2(√6))(t^2 −(2(√2)+((4(√3))/3))t+5+2(√6))))dt now do the decomposition yourself!!!!!!!!](https://www.tinkutara.com/question/Q156851.png)
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{3}}{t}^{\mathrm{2}} −\mathrm{2}{t}−\sqrt{\mathrm{3}}}{\mathrm{4}{t}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}}{\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}\right] \\ $$$$=\frac{\mathrm{16}}{\mathrm{3}}\int\frac{{t}}{{t}^{\mathrm{4}} −\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}{t}^{\mathrm{3}} +\frac{\mathrm{22}}{\mathrm{3}}{t}^{\mathrm{2}} +\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}{t}+\mathrm{1}}{dt}= \\ $$$$=\frac{\mathrm{16}}{\mathrm{3}}\int\frac{{t}}{\left({t}^{\mathrm{2}} −\left(\mathrm{2}\sqrt{\mathrm{2}}−\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\right){t}+\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)\left({t}^{\mathrm{2}} −\left(\mathrm{2}\sqrt{\mathrm{2}}+\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\right){t}+\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)}{dt} \\ $$$$\mathrm{now}\:\mathrm{do}\:\mathrm{the}\:\mathrm{decomposition}\:\mathrm{yourself}!!!!!!!! \\ $$
Commented by tabata last updated on 16/Oct/21

$$\boldsymbol{{its}}\:\boldsymbol{{very}}\:\boldsymbol{{hard}}\:\boldsymbol{{question}} \\ $$
