Menu Close

dx-x-2-x-3-1-1-3-

Tinku Tara 0 Comments
Pin




Question Number 104388 by Ar Brandon last updated on 21/Jul/20
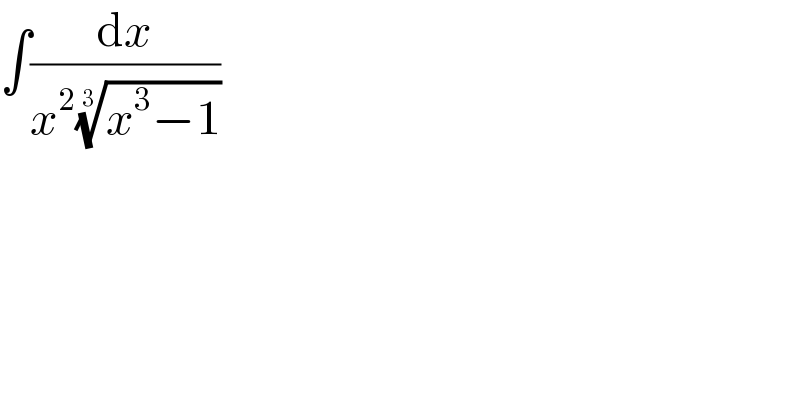
∫(dx/(x^2 ((x^3 −1))^(1/3) ))
$$\int\frac{\mathrm{d}{x}}{{x}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{1}}} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Jul/20
∫(dx/(x^3 (1−(1/x^3 ))^(1/3) ))=∫(((1/x^4 ).x)/((1−(1/x^3 ))^(1/3) ))dx=(x/3)∫((3/x^4 )/((1−(1/x^3 ))^(1/3) ))−(1/3)∫∫((3/x^4 )/((1−(1/x^3 ))^(1/3) )) =(x/2)(1−(1/x^3 ))^(2/3) −(1/2)∫(1−(1/x^3 ))^(2/3) =(x/2)(1−(1/x^3 ))^(2/3) −(1/2) ∫(3/x^4 ).(x^4 /3)(1−(1/x^3 ))^(2/3) dx (x/2)(1−(1/x^3 ))^(2/3) −(1/6)∫x^4 t^(2/3) dt {1−(1/x^3 )=t x^3 =(1/(1−t)) (x/2)(1−(1/x^3 ))−(1/6)∫((1/(1−t)))^(4/3) t^(2/3) .....continue
$$\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }=\int\frac{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }.\mathrm{x}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }\mathrm{dx}=\frac{\mathrm{x}}{\mathrm{3}}\int\frac{\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{4}} }}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }−\frac{\mathrm{1}}{\mathrm{3}}\int\int\frac{\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{4}} }}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$=\frac{\mathrm{x}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{2}}{\mathrm{3}}} −\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{x}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{2}}{\mathrm{3}}} −\frac{\mathrm{1}}{\mathrm{2}}\:\int\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{4}} }.\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \mathrm{dx} \\ $$$$\frac{\mathrm{x}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{2}}{\mathrm{3}}} −\frac{\mathrm{1}}{\mathrm{6}}\int\mathrm{x}^{\mathrm{4}} \mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}} \mathrm{dt}\:\:\:\:\:\:\:\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }=\mathrm{t}\:\:\mathrm{x}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{1}−\mathrm{t}}\right. \\ $$$$\frac{\mathrm{x}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)−\frac{\mathrm{1}}{\mathrm{6}}\int\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{t}}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\:\:…..\mathrm{continue} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *