Menu Close

dx-x-2021-1-x-2020-

Tinku Tara 0 Comments
Pin




Question Number 127618 by bramlexs22 last updated on 31/Dec/20
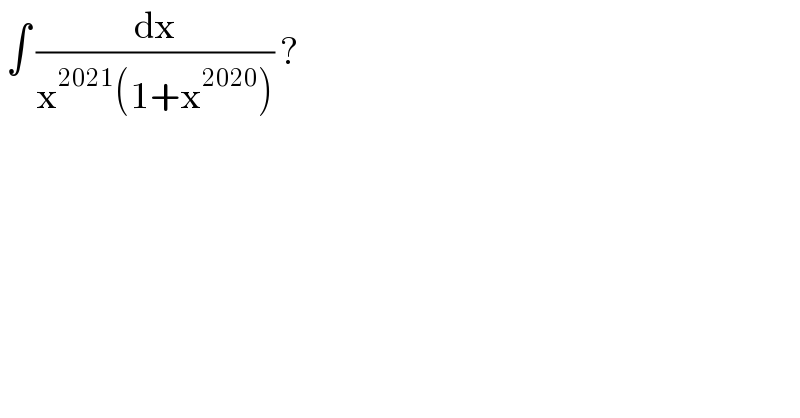
∫ (dx/(x^(2021) (1+x^(2020) ))) ?
$$\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2021}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2020}} \right)}\:?\: \\ $$
Answered by Dwaipayan Shikari last updated on 31/Dec/20
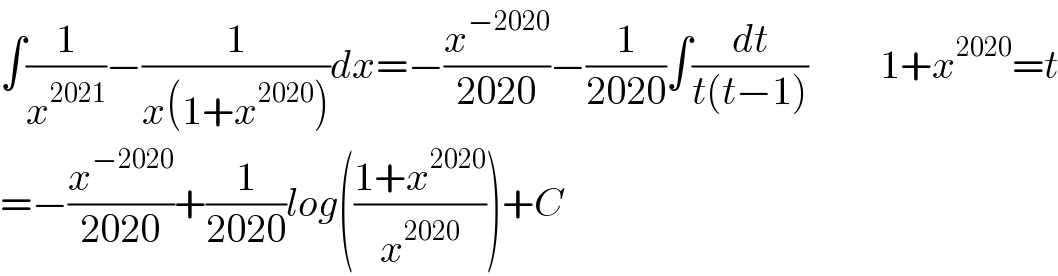
∫(1/x^(2021) )−(1/(x(1+x^(2020) )))dx=−(x^(−2020) /(2020))−(1/(2020))∫(dt/(t(t−1))) 1+x^(2020) =t =−(x^(−2020) /(2020))+(1/(2020))log(((1+x^(2020) )/x^(2020) ))+C
$$\int\frac{\mathrm{1}}{{x}^{\mathrm{2021}} }−\frac{\mathrm{1}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2020}} \right)}{dx}=−\frac{{x}^{−\mathrm{2020}} }{\mathrm{2020}}−\frac{\mathrm{1}}{\mathrm{2020}}\int\frac{{dt}}{{t}\left({t}−\mathrm{1}\right)}\:\:\:\:\:\:\:\:\:\mathrm{1}+{x}^{\mathrm{2020}} ={t} \\ $$$$=−\frac{{x}^{−\mathrm{2020}} }{\mathrm{2020}}+\frac{\mathrm{1}}{\mathrm{2020}}{log}\left(\frac{\mathrm{1}+{x}^{\mathrm{2020}} }{{x}^{\mathrm{2020}} }\right)+{C} \\ $$
Commented by Dwaipayan Shikari last updated on 31/Dec/20
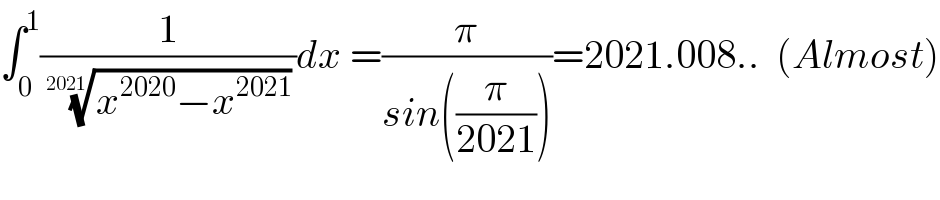
∫_0 ^1 (1/( ((x^(2020) −x^(2021) ))^(1/(2021)) ))dx =(π/(sin((π/(2021)))))=2021.008.. (Almost)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt[{\mathrm{2021}}]{{x}^{\mathrm{2020}} −{x}^{\mathrm{2021}} }}{dx}\:=\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{2021}}\right)}=\mathrm{2021}.\mathrm{008}..\:\:\left({Almost}\right) \\ $$
Commented by bramlexs22 last updated on 31/Dec/20
Happy New Year 2021
$$\mathrm{Happy}\:\mathrm{New}\:\mathrm{Year}\:\mathrm{2021} \\ $$
Commented by Dwaipayan Shikari last updated on 31/Dec/20
Happy new year too..
$${Happy}\:{new}\:{year}\:{too}.. \\ $$
Answered by liberty last updated on 31/Dec/20
L = ∫ (dx/(x^(2021) (1+x^(2020) ))) = ∫ (((x^(2020) +1)−x^(2020) )/(x^(2021) (1+x^(2020) ))) dx L = ∫ ((x^(2020) +1)/(x^(2021) (1+x^(2020) )))dx−∫ (x^(2020) /(x^(2021) (1+x^(2020) )))dx L = ∫ x^(−2021) dx −∫ (dx/(x(1+x^(2020) ))) L=−(1/(2020x^(2020) )) −∫ (dx/(x^(2021) (1+x^(−2020) ))) let L_1 = ∫ (x^(−2021) /(1+x^(−2020) )) dx put 1+x^(−2020) = w and −2020x^(−2021) dx=dw we find L_1 = −(1/(2020)) ∫ (dw/w) = −(1/(2020)) ln ∣w∣ + c thus we complete the integral has solution L = −(1/(2020 x^(2020) )) + ((ln (((1+x^(2020) )/x^(2020) )))/(2020)) + C L = −(1/(2020 x^(2020) ))+ (1/(2020)) ln (1+x^(2020) )−ln (x) + C
$$\:\mathrm{L}\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2021}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2020}} \right)}\:=\:\int\:\frac{\left(\mathrm{x}^{\mathrm{2020}} +\mathrm{1}\right)−\mathrm{x}^{\mathrm{2020}} }{\mathrm{x}^{\mathrm{2021}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2020}} \right)}\:\mathrm{dx} \\ $$$$\mathrm{L}\:=\:\int\:\frac{\mathrm{x}^{\mathrm{2020}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2021}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2020}} \right)}\mathrm{dx}−\int\:\frac{\mathrm{x}^{\mathrm{2020}} }{\mathrm{x}^{\mathrm{2021}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2020}} \right)}\mathrm{dx} \\ $$$$\mathrm{L}\:=\:\int\:\mathrm{x}^{−\mathrm{2021}} \:\mathrm{dx}\:−\int\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2020}} \right)} \\ $$$$\mathrm{L}=−\frac{\mathrm{1}}{\mathrm{2020x}^{\mathrm{2020}} }\:−\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2021}} \left(\mathrm{1}+\mathrm{x}^{−\mathrm{2020}} \right)} \\ $$$$\mathrm{let}\:\mathrm{L}_{\mathrm{1}} =\:\int\:\frac{\mathrm{x}^{−\mathrm{2021}} }{\mathrm{1}+\mathrm{x}^{−\mathrm{2020}} }\:\mathrm{dx} \\ $$$$\:\mathrm{put}\:\mathrm{1}+\mathrm{x}^{−\mathrm{2020}} \:=\:\mathrm{w}\:\mathrm{and}\:−\mathrm{2020x}^{−\mathrm{2021}} \:\mathrm{dx}=\mathrm{dw} \\ $$$$\mathrm{we}\:\mathrm{find}\:\mathrm{L}_{\mathrm{1}} =\:−\frac{\mathrm{1}}{\mathrm{2020}}\:\int\:\frac{\mathrm{dw}}{\mathrm{w}}\:=\:−\frac{\mathrm{1}}{\mathrm{2020}}\:\mathrm{ln}\:\mid\mathrm{w}\mid\:+\:\mathrm{c} \\ $$$$\mathrm{thus}\:\mathrm{we}\:\mathrm{complete}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{has} \\ $$$$\mathrm{solution}\:\mathrm{L}\:=\:−\frac{\mathrm{1}}{\mathrm{2020}\:\mathrm{x}^{\mathrm{2020}} }\:+\:\frac{\mathrm{ln}\:\left(\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2020}} }{\mathrm{x}^{\mathrm{2020}} }\right)}{\mathrm{2020}}\:+\:\mathrm{C} \\ $$$$\mathrm{L}\:=\:−\frac{\mathrm{1}}{\mathrm{2020}\:\mathrm{x}^{\mathrm{2020}} }+\:\frac{\mathrm{1}}{\mathrm{2020}}\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2020}} \right)−\mathrm{ln}\:\left(\mathrm{x}\right)\:+\:\mathrm{C}\: \\ $$
Commented by bramlexs22 last updated on 31/Dec/20
Happy New Year 2021
$$\mathrm{Happy}\:\mathrm{New}\:\mathrm{Year}\:\mathrm{2021} \\ $$
Commented by liberty last updated on 31/Dec/20
Happy New Year too
$$\boldsymbol{\mathrm{H}}\mathrm{appy}\:\boldsymbol{\mathrm{N}}\mathrm{ew}\:\boldsymbol{\mathrm{Y}}\mathrm{ear}\:\boldsymbol{\mathrm{too}}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *