Menu Close

dx-x-2n-1-x-n-1-

Tinku Tara 0 Comments
Pin




Question Number 129646 by liberty last updated on 17/Jan/21
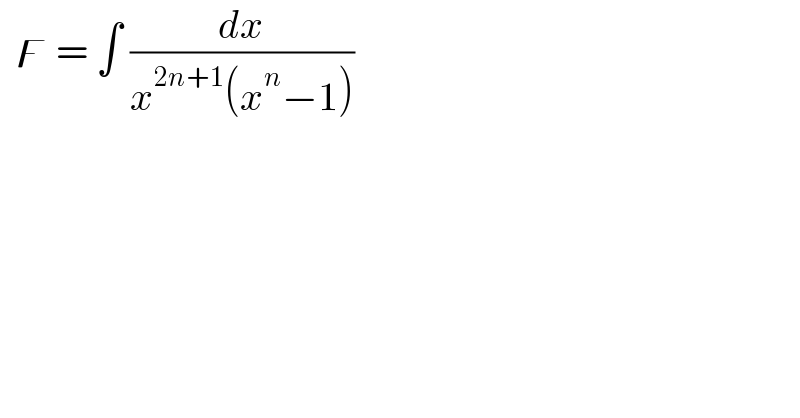
ϝ = ∫ (dx/(x^(2n+1) (x^n −1)))
$$\:\:\digamma\:=\:\int\:\frac{{dx}}{{x}^{\mathrm{2}{n}+\mathrm{1}} \left({x}^{{n}} −\mathrm{1}\right)} \\ $$
Answered by TheSupreme last updated on 17/Jan/21
x^n =t x=t^(1/n) x^(2n+1) =t^(2+(1/n)) dx=(1/n)t^((1/n)−1) dt ∫(((1/n)t^((1/n)−1) )/(t^(2+(1/n)) (t−1)))=∫(1/n) (1/(t^3 (t−1)))dt ((At^2 +Bt+C)/t^3 )+(D/(t−1))=(1/D) { (((t^3 ) A+D=0)),(((t^2 ) B−A=0)),(((t) −B+C=0)),(((1) −C=1)) :} F=(1/n)∫−((t^2 +t+1)/t^3 )+(1/(t−1)) dt F=(1/n)∫−(1/t)−(1/t^2 )−(1/t^3 )+(1/(t−1))dt F=(1/n)[−log(t)+(1/t)+(1/(2t^2 ))+log(t−1)+c] F=(1/n)log((x^n −1)/x^n ) +(1/x^n )+(1/(2x^(2n) ))+c
$${x}^{{n}} ={t} \\ $$$${x}={t}^{\frac{\mathrm{1}}{{n}}} \\ $$$${x}^{\mathrm{2}{n}+\mathrm{1}} ={t}^{\mathrm{2}+\frac{\mathrm{1}}{{n}}} \\ $$$${dx}=\frac{\mathrm{1}}{{n}}{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dt} \\ $$$$ \\ $$$$\int\frac{\frac{\mathrm{1}}{{n}}{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{{t}^{\mathrm{2}+\frac{\mathrm{1}}{{n}}} \left({t}−\mathrm{1}\right)}=\int\frac{\mathrm{1}}{{n}}\:\frac{\mathrm{1}}{{t}^{\mathrm{3}} \left({t}−\mathrm{1}\right)}{dt} \\ $$$$\frac{{At}^{\mathrm{2}} +{Bt}+{C}}{{t}^{\mathrm{3}} }+\frac{{D}}{{t}−\mathrm{1}}=\frac{\mathrm{1}}{{D}} \\ $$$$\begin{cases}{\left({t}^{\mathrm{3}} \right)\:{A}+{D}=\mathrm{0}}\\{\left({t}^{\mathrm{2}} \right)\:{B}−{A}=\mathrm{0}}\\{\left({t}\right)\:−{B}+{C}=\mathrm{0}}\\{\left(\mathrm{1}\right)\:−{C}=\mathrm{1}}\end{cases} \\ $$$${F}=\frac{\mathrm{1}}{{n}}\int−\frac{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{{t}^{\mathrm{3}} }+\frac{\mathrm{1}}{{t}−\mathrm{1}}\:{dt} \\ $$$${F}=\frac{\mathrm{1}}{{n}}\int−\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }+\frac{\mathrm{1}}{{t}−\mathrm{1}}{dt} \\ $$$${F}=\frac{\mathrm{1}}{{n}}\left[−{log}\left({t}\right)+\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }+{log}\left({t}−\mathrm{1}\right)+{c}\right] \\ $$$${F}=\frac{\mathrm{1}}{{n}}\mathrm{log}\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }+\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2n}} }+\mathrm{c} \\ $$$$ \\ $$
Answered by liberty last updated on 17/Jan/21
ϝ = −(1/(2n)) ∫ (1/(x^n −1)) d((1/x^(2n) )) ϝ = −(1/(2n))∫ ((1/x^n )/(1−(1/x^n ))) d((1/x^(2n) )) let (1/x^n ) = r ⇒r^2 = (1/x^(2n) ) ∧ 2r dr = d((1/x^(2n) )) ϝ = −(1/(2n))∫ (r/(1−r)) (2r dr ) ϝ = −(1/n)∫ ((1−(1−r^2 ))/(1−r)) dr ϝ = (1/n) [ ln ∣1−r∣ +∫ (1+r) dr ] ϝ = (1/n) [ ln ∣1−(1/x^n )∣+(1/x^n )+(1/(2x^(2n) )) ] + C
$$\:\digamma\:=\:−\frac{\mathrm{1}}{\mathrm{2n}}\:\int\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} −\mathrm{1}}\:\mathrm{d}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2n}} }\right)\: \\ $$$$\:\digamma\:=\:−\frac{\mathrm{1}}{\mathrm{2n}}\int\:\frac{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }}\:\mathrm{d}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2n}} }\right) \\ $$$$\:\mathrm{let}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\:=\:{r}\:\Rightarrow{r}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }\:\wedge\:\mathrm{2}{r}\:{dr}\:=\:{d}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}} }\right) \\ $$$$\:\digamma\:=\:−\frac{\mathrm{1}}{\mathrm{2n}}\int\:\frac{{r}}{\mathrm{1}−{r}}\:\left(\mathrm{2}{r}\:{dr}\:\right) \\ $$$$\:\digamma\:=\:−\frac{\mathrm{1}}{\mathrm{n}}\int\:\frac{\mathrm{1}−\left(\mathrm{1}−{r}^{\mathrm{2}} \right)}{\mathrm{1}−{r}}\:{dr}\: \\ $$$$\:\digamma\:=\:\frac{\mathrm{1}}{\mathrm{n}}\:\left[\:\mathrm{ln}\:\mid\mathrm{1}−{r}\mid\:+\int\:\left(\mathrm{1}+{r}\right)\:{dr}\:\right]\: \\ $$$$\:\digamma\:=\:\frac{\mathrm{1}}{\mathrm{n}}\:\left[\:\mathrm{ln}\:\mid\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\mid+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }+\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2n}} }\:\right]\:+\:\mathrm{C}\: \\ $$
Answered by mathmax by abdo last updated on 17/Jan/21
I=∫ (dx/(x^(2n+1) (x^n −1))) changement x=t^(1/n) give I=(1/n)∫ (t^((1/n)−1) /(t^((2n+1)/n) (t−1)))dt =(1/n)∫ ((t^((1/n)−1) .t^(−2−(1/n)) )/(t−1))dt =(1/n)∫ (dt/(t^3 (t−1))) let decompose F(t)=(1/(t^3 (t−1))) F(t)=(a/t)+(b/t^2 )+(c/t^3 ) +(d/(t−1)) c=−1 ,d=1 ⇒F(t)=(a/t)+(b/t^2 )−(1/t^3 )+(1/(t−1)) lim_(t→+∞) tF(t)=0=a+1 ⇒a=−1 ⇒F(t)=−(1/t)+(b/t^2 )−(1/t^3 )+(1/(t−1)) F(−1)=(1/2)=1+b+1−(1/2)=b+2−(1/2)=b+(3/2) ⇒b=(1/2)−(3/2)=−1 ⇒ F(t)=−(1/t)−(1/t^2 )−(1/t^3 )+(1/(t−1)) ⇒∫ F(t)dt=−ln∣t∣+(1/t)+(1/(2t^2 ))+ln∣t−1∣ +C =ln∣((t−1)/t)∣+(1/t)+(1/(2t^2 )) +C =ln∣((x^n −1)/x^n )∣+(1/x^n ) +(1/(2x^(2n) )) +C
$$\mathrm{I}=\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \left(\mathrm{x}^{\mathrm{n}} −\mathrm{1}\right)}\:\mathrm{changement}\:\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}} \:\mathrm{give} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{n}}\int\:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} }{\mathrm{t}^{\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{n}}} \left(\mathrm{t}−\mathrm{1}\right)}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{n}}\int\:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} .\mathrm{t}^{−\mathrm{2}−\frac{\mathrm{1}}{\mathrm{n}}} }{\mathrm{t}−\mathrm{1}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{3}} \left(\mathrm{t}−\mathrm{1}\right)}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} \left(\mathrm{t}−\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}}{\mathrm{t}}+\frac{\mathrm{b}}{\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{c}}{\mathrm{t}^{\mathrm{3}} }\:+\frac{\mathrm{d}}{\mathrm{t}−\mathrm{1}} \\ $$$$\mathrm{c}=−\mathrm{1}\:,\mathrm{d}=\mathrm{1}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}}{\mathrm{t}}+\frac{\mathrm{b}}{\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)=\mathrm{0}=\mathrm{a}+\mathrm{1}\:\Rightarrow\mathrm{a}=−\mathrm{1}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=−\frac{\mathrm{1}}{\mathrm{t}}+\frac{\mathrm{b}}{\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}} \\ $$$$\mathrm{F}\left(−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{1}+\mathrm{b}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{b}+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{b}+\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\mathrm{b}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=−\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}\:\Rightarrow\int\:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}=−\mathrm{ln}\mid\mathrm{t}\mid+\frac{\mathrm{1}}{\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }+\mathrm{ln}\mid\mathrm{t}−\mathrm{1}\mid\:+\mathrm{C} \\ $$$$=\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}}\mid+\frac{\mathrm{1}}{\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\:+\mathrm{C}\:=\mathrm{ln}\mid\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\mid+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\:+\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2n}} }\:+\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 17/Jan/21
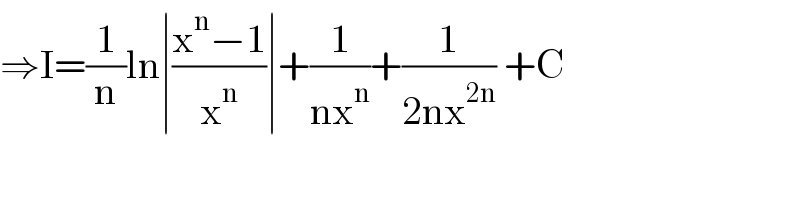
⇒I=(1/n)ln∣((x^n −1)/x^n )∣+(1/(nx^n ))+(1/(2nx^(2n) )) +C
$$\Rightarrow\mathrm{I}=\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\mid\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\mid+\frac{\mathrm{1}}{\mathrm{nx}^{\mathrm{n}} }+\frac{\mathrm{1}}{\mathrm{2nx}^{\mathrm{2n}} }\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *