Question Number 81684 by naka3546 last updated on 14/Feb/20
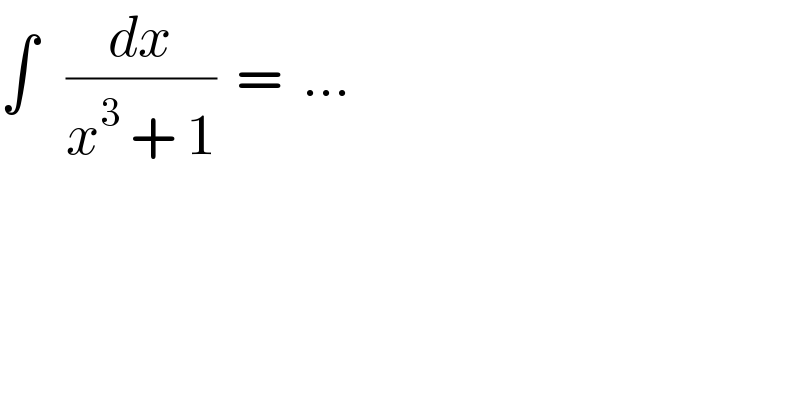
$$\int\:\:\:\frac{{dx}}{{x}^{\mathrm{3}} \:+\:\mathrm{1}}\:\:=\:\:… \\ $$
Commented by Tony Lin last updated on 14/Feb/20
![∫ (dx/(x^3 +1)) =∫(dx/((x+1)(x^2 −x+1))) =(1/3)∫(1/(x+1 ))dx−(1/3)∫((x−2)/(x^2 −x+1))dx =(1/3)ln∣x+1∣−(1/3)[∫(((1/2)(2x−1))/(x^2 −x+1)) dx−(3/2)∫(dx/((x−(1/2))^2 +(3/4)))] =(1/3)ln∣x+1∣−(1/6)ln∣x^2 −x+1∣+(√3)tan^(−1) (((2x−1)/( (√3))))+c](https://www.tinkutara.com/question/Q81687.png)
$$\int\:\frac{{dx}}{{x}^{\mathrm{3}} +\mathrm{1}} \\ $$$$=\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{{x}+\mathrm{1}\:\:}{dx}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{3}}\left[\int\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{dx}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid+\sqrt{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{c} \\ $$
Answered by TANMAY PANACEA last updated on 14/Feb/20

$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}=\int\frac{{a}}{{x}+\mathrm{1}}{dx}+\int\frac{{bx}+{c}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$${now} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{3}} +\mathrm{1}}=\frac{{ax}^{\mathrm{2}} −{ax}+{a}+{bx}^{\mathrm{2}} +{bx}+{cx}+{c}}{{x}^{\mathrm{3}} +\mathrm{1}} \\ $$$$\mathrm{1}={x}^{\mathrm{2}} \left({a}+{b}\right)+{x}\left(−{a}+{b}+{c}\right)+{a}+{c} \\ $$$${a}+{b}=\mathrm{0} \\ $$$$−{a}+{b}+{c}=\mathrm{0} \\ $$$${a}+{c}=\mathrm{1}\:\: \\ $$$$−{a}+\left(−{a}\right)+\left(\mathrm{1}−{a}\right)=\mathrm{0} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:{b}=\frac{−\mathrm{1}}{\mathrm{3}}\:\:\:{c}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\int\frac{\frac{\mathrm{1}}{\mathrm{3}}}{{x}+\mathrm{1}}{dx}+\int\frac{\frac{−\mathrm{1}}{\mathrm{3}}{x}+\frac{\mathrm{2}}{\mathrm{3}}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{3}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{d}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}.{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{d}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{ln}\left({x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right) \\ $$$${pls}\:{check} \\ $$$$ \\ $$
Commented by peter frank last updated on 14/Feb/20
$${welcom}\:{again}\:{mr}\:{tanymay},…. \\ $$$${long}\:{time}\: \\ $$
