dx-x-3-1-x-2-

Question Number 144409 by liberty last updated on 25/Jun/21

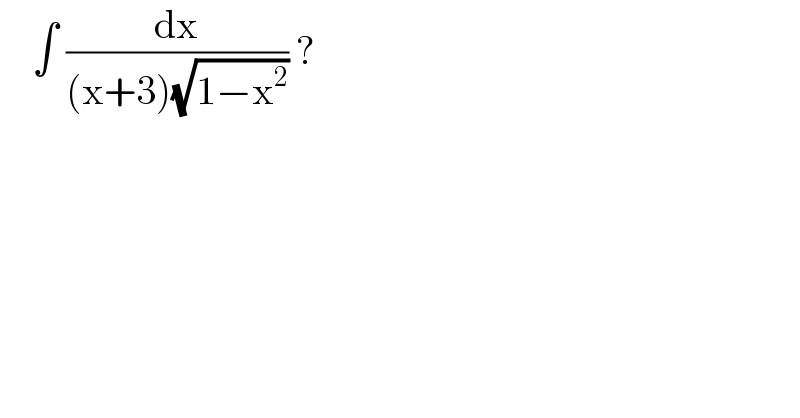
$$\:\:\:\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{3}\right)\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:? \\ $$

Answered by iloveisrael last updated on 25/Jun/21

let x=sin t I=∫ ((cos t)/((3+sin t)(√(1−sin^2 t)))) dt I= ∫ (dt/(3+sin t)) let tan ((t/2))=u ⇒ dt =(2/(1+u^2 )) du I=∫((2/(1+u^2 )))((1/(3+((2u)/(1+u^2 )))))du I=∫(2/(3u^2 +2u+3)) du I=(2/3)∫ (du/(u^2 +(2/3)u+1)) I=(2/3)∫ (du/((u+(1/3))^2 +(8/9))) I=(2/3)∫ (du/((u+(1/3))^2 +(((2(√2))/3))^2 ))

$$\:\mathrm{let}\:\mathrm{x}=\mathrm{sin}\:\mathrm{t}\: \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{cos}\:\mathrm{t}}{\left(\mathrm{3}+\mathrm{sin}\:\mathrm{t}\right)\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{t}}}\:\mathrm{dt} \\ $$$$\mathrm{I}=\:\int\:\frac{\mathrm{dt}}{\mathrm{3}+\mathrm{sin}\:\mathrm{t}} \\ $$$$\mathrm{let}\:\mathrm{tan}\:\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}\: \\ $$$$\Rightarrow\:\mathrm{dt}\:=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:\mathrm{du} \\ $$$$\mathrm{I}=\int\left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}\right)\mathrm{du} \\ $$$$\mathrm{I}=\int\frac{\mathrm{2}}{\mathrm{3u}^{\mathrm{2}} +\mathrm{2u}+\mathrm{3}}\:\mathrm{du} \\ $$$$\mathrm{I}=\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{3}}\mathrm{u}+\mathrm{1}} \\ $$$$\mathrm{I}=\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\mathrm{du}}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{8}}{\mathrm{9}}} \\ $$$$\mathrm{I}=\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\mathrm{du}}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{\mathrm{2}} }\: \\ $$

Answered by mathmax by abdo last updated on 25/Jun/21

Ψ=∫ (dx/((x+3)(√(1−x^2 )))) changement x=sint give Ψ=∫ ((cost dt)/((sint+3)cost))=∫ (dt/(3+sint))=_(tan((t/2))=y) ∫ ((2dy)/((1+y^2 )(3+((2y)/(1+y^2 ))))) =∫ ((2dy)/(3+3y^2 +2y))=∫ ((2dy)/(3y^2 +2y+3)) =(2/3)∫ (dy/(y^2 +(2/3)y +1))=(2/3)∫ (dy/(y^2 +(2/3)y +(1/9)+1−(1/9))) =(2/3)∫ (dy/((y+(1/3))^2 +(8/9)))=_(y+(1/3)=((2(√2))/3)z) (2/3)×(9/8)∫ (1/(z^2 +1))×((2(√2))/3)dz =((√2)/2)arcctanz +K =((√2)/2)arctan(((3y+1)/(2(√2))))+K =((√2)/2)arctan(((3tan((t/2))+1)/(2(√2))))+K Ψ=((√2)/2)arctan(((3tan(((arcsinx)/2))+1)/(2(√2))))+K

$$\Psi=\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{3}\right)\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{changement}\:\mathrm{x}=\mathrm{sint}\:\mathrm{give} \\ $$$$\Psi=\int\:\:\frac{\mathrm{cost}\:\mathrm{dt}}{\left(\mathrm{sint}+\mathrm{3}\right)\mathrm{cost}}=\int\:\frac{\mathrm{dt}}{\mathrm{3}+\mathrm{sint}}=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{y}} \:\:\int\:\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{3}+\frac{\mathrm{2y}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }\right)} \\ $$$$=\int\:\frac{\mathrm{2dy}}{\mathrm{3}+\mathrm{3y}^{\mathrm{2}} \:+\mathrm{2y}}=\int\:\frac{\mathrm{2dy}}{\mathrm{3y}^{\mathrm{2}} \:+\mathrm{2y}+\mathrm{3}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\:\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} \:+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{y}\:+\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} \:+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{y}\:+\frac{\mathrm{1}}{\mathrm{9}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{9}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\mathrm{dy}}{\left(\mathrm{y}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{8}}{\mathrm{9}}}=_{\mathrm{y}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{z}} \:\:\:\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{9}}{\mathrm{8}}\int\:\:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}×\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{dz} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arcctanz}\:+\mathrm{K}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{3y}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)+\mathrm{K} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{3tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)+\mathrm{K} \\ $$$$\Psi=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{3tan}\left(\frac{\mathrm{arcsinx}}{\mathrm{2}}\right)+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)+\mathrm{K} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply