Question Number 183157 by cortano1 last updated on 21/Dec/22
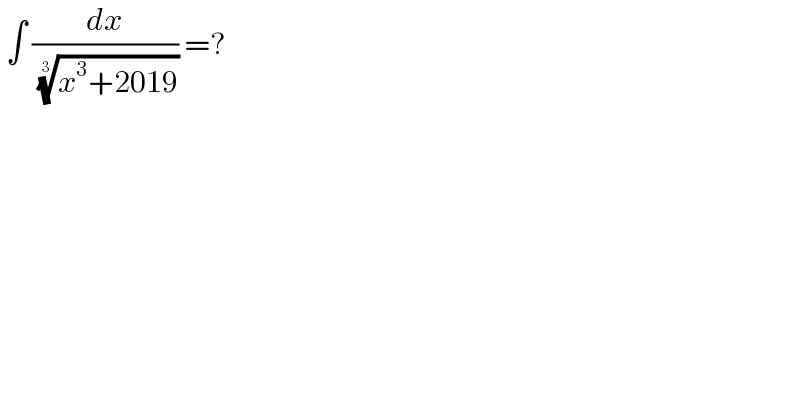
$$\:\int\:\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +\mathrm{2019}}}\:=? \\ $$
Answered by MJS_new last updated on 21/Dec/22
![∫(dx/( ((x^3 +a))^(1/3) ))= [t=(x/( ((x^3 +a))^(1/3) )) → dx=((((x^3 +a)^4 ))^(1/3) /a)] =∫(dt/(1−t^3 ))= [the usual method] =(1/6)ln (t^2 +t+1) +(1/3)ln (t−1) +((√3)/3)arctan (((√3)(2t+1))/3) now insert](https://www.tinkutara.com/question/Q183160.png)
$$\int\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{a}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}}{\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{a}}}\:\rightarrow\:{dx}=\frac{\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{3}} +{a}\right)^{\mathrm{4}} }}{{a}}\right] \\ $$$$=\int\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{3}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{the}\:\mathrm{usual}\:\mathrm{method}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\mathrm{now}\:\mathrm{insert} \\ $$
