Question Number 106830 by malwaan last updated on 08/Aug/20

$$\int\frac{\:{dx}}{\:\sqrt{{x}^{\mathrm{3}} \:}\:\:^{\mathrm{3}} \sqrt{\mathrm{1}\:+\:^{\mathrm{4}} \sqrt{{x}^{\mathrm{3}} }}}\:=\:? \\ $$
Commented by mathmax by abdo last updated on 07/Aug/20

$$\mathrm{its}\:\mathrm{seems}\:\mathrm{that}\:\int\:\frac{\mathrm{tdt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\mathrm{is}\:\mathrm{not}\:\mathrm{solvable}\:…! \\ $$
Commented by bobhans last updated on 07/Aug/20
![∫ (dx/( (x^2 )^(1/4) ((1+(x^3 )^(1/4) ))^(1/3) )) [ let (x)^(1/4) = t ] ∫ ((4t^3 dt)/(t^2 ((1+t^3 ))^(1/3) )) = ∫ ((4t)/( ((1+t^3 ))^(1/3) )) dt next...](https://www.tinkutara.com/question/Q106839.png)
$$\int\:\frac{\mathrm{dx}}{\:\sqrt[{\mathrm{4}}]{\mathrm{x}^{\mathrm{2}} }\:\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt[{\mathrm{4}}]{\mathrm{x}^{\mathrm{3}} }}}\:\left[\:\mathrm{let}\:\sqrt[{\mathrm{4}}]{\mathrm{x}}\:=\:\mathrm{t}\:\right] \\ $$$$\int\:\frac{\mathrm{4t}^{\mathrm{3}} \:\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{t}^{\mathrm{3}} }}\:=\:\int\:\frac{\mathrm{4t}}{\:\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{t}^{\mathrm{3}} }}\:\mathrm{dt}\: \\ $$$$\mathrm{next}… \\ $$
Commented by Her_Majesty last updated on 07/Aug/20
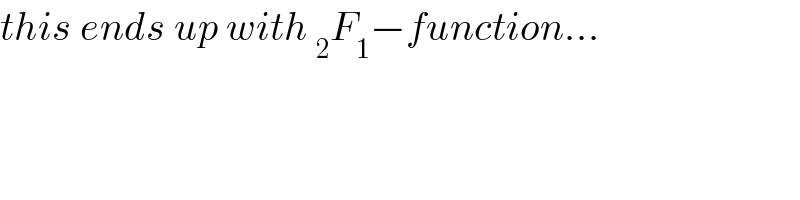
$${this}\:{ends}\:{up}\:{with}\:_{\mathrm{2}} {F}_{\mathrm{1}} −{function}… \\ $$
Commented by malwaan last updated on 07/Aug/20

$${this}\:{is}\:{for}\:{secondary}\:{schools} \\ $$$${your}−{majesty} \\ $$
Commented by Sarah85 last updated on 07/Aug/20

$$\int\:\frac{{t}}{\:\sqrt[{\mathrm{3}}]{\mathrm{1}+{t}^{\mathrm{3}} }}\:{dt}=_{\mathrm{2}} {F}_{\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{3}};\:\frac{\mathrm{2}}{\mathrm{3}};\:\frac{\mathrm{5}}{\mathrm{3}};\:−{t}^{\mathrm{3}} \right)\:×\frac{{t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{Her}\:\mathrm{Majesty}\:\mathrm{is}\:\mathrm{right} \\ $$
Commented by malwaan last updated on 08/Aug/20

$${I}=\:\int\:{x}^{−\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}+\:{x}^{\frac{\mathrm{3}}{\mathrm{4}}} \right)^{−\frac{\mathrm{1}}{\mathrm{3}}} {dx} \\ $$$${t}\:=\:\left(\frac{\mathrm{1}+\:{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }{{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${I}\:{think}\:{we}\:{will}\:{get}\:{the}\:{solution} \\ $$$${with}\:{elementary}\:{functions} \\ $$
Commented by malwaan last updated on 08/Aug/20
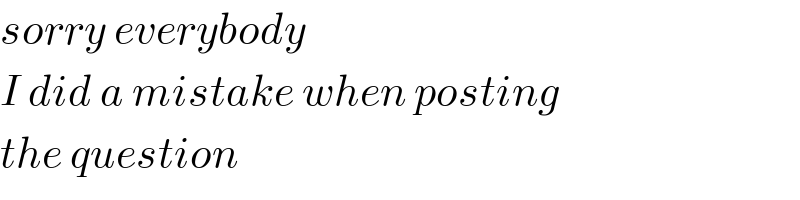
$${sorry}\:{everybody} \\ $$$${I}\:{did}\:{a}\:{mistake}\:{when}\:{posting} \\ $$$${the}\:{question} \\ $$
Answered by malwaan last updated on 08/Aug/20
![I= ∫ x^(−(2/3)) (1+x^(3/4) )^(−(1/3)) dx t=(((1+x^(3/4) )/x^(3/4) ))^(1/3) =(1+x^(−(3/4)) ) t^3 =1+x^(−(3/4)) x^(−(3/4)) = t^3 −1 ; x^(3/4) = (1/(t^3 −1)) x = (t^3 −1)^(−(4/3)) ⇒dx = −4t^2 (t^3 −1)^(−(7/3)) dt ∫[(t^3 −1)^(−(4/3)) ]^(−(3/2)) [1+(1/(t^3 −1))]^(−(1/3)) (−4t^2 )(t^3 −1)^(−(7/3)) dt = −4∫ t^2 (t^3 −1)^2 t^(−1) (t^3 −1)^(1/3) (t^3 −1)^(−(7/3)) dt = −4∫ tdt = −4(t^2 /2) + C = −2t^2 + C = −2 ^3 (√((1+ x^(−(3/4)) )^2 )) + C](https://www.tinkutara.com/question/Q106981.png)
$${I}=\:\int\:{x}^{−\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}+{x}^{\frac{\mathrm{3}}{\mathrm{4}}} \right)^{−\frac{\mathrm{1}}{\mathrm{3}}} {dx} \\ $$$${t}=\left(\frac{\mathrm{1}+{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }{{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\left(\mathrm{1}+{x}^{−\frac{\mathrm{3}}{\mathrm{4}}} \right) \\ $$$${t}^{\mathrm{3}} =\mathrm{1}+{x}^{−\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$${x}^{−\frac{\mathrm{3}}{\mathrm{4}}} =\:{t}^{\mathrm{3}} −\mathrm{1}\:;\:{x}^{\frac{\mathrm{3}}{\mathrm{4}}} =\:\frac{\mathrm{1}}{{t}^{\mathrm{3}} −\mathrm{1}} \\ $$$${x}\:=\:\left({t}^{\mathrm{3}} \:−\mathrm{1}\right)^{−\frac{\mathrm{4}}{\mathrm{3}}} \\ $$$$\Rightarrow{dx}\:=\:−\mathrm{4}{t}^{\mathrm{2}} \left({t}^{\mathrm{3}} −\mathrm{1}\right)^{−\frac{\mathrm{7}}{\mathrm{3}}} {dt} \\ $$$$\int\left[\left({t}^{\mathrm{3}} −\mathrm{1}\right)^{−\frac{\mathrm{4}}{\mathrm{3}}} \right]^{−\frac{\mathrm{3}}{\mathrm{2}}} \left[\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{3}} −\mathrm{1}}\right]^{−\frac{\mathrm{1}}{\mathrm{3}}} \left(−\mathrm{4}{t}^{\mathrm{2}} \right)\left({t}^{\mathrm{3}} −\mathrm{1}\right)^{−\frac{\mathrm{7}}{\mathrm{3}}} {dt} \\ $$$$=\:−\mathrm{4}\int\:{t}^{\mathrm{2}} \left({t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} {t}^{−\mathrm{1}} \left({t}^{\mathrm{3}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \left({t}^{\mathrm{3}} −\mathrm{1}\right)^{−\frac{\mathrm{7}}{\mathrm{3}}} {dt} \\ $$$$=\:−\mathrm{4}\int\:{tdt}\:=\:−\mathrm{4}\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:+\:{C} \\ $$$$=\:−\mathrm{2}{t}^{\mathrm{2}} \:+\:{C} \\ $$$$=\:−\mathrm{2}\:\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\:{x}^{−\frac{\mathrm{3}}{\mathrm{4}}} \right)^{\mathrm{2}} }\:\:+\:{C} \\ $$
