Menu Close

dx-x-3-3x-5-

Tinku Tara 0 Comments
Pin




Question Number 102922 by mohammad17 last updated on 11/Jul/20
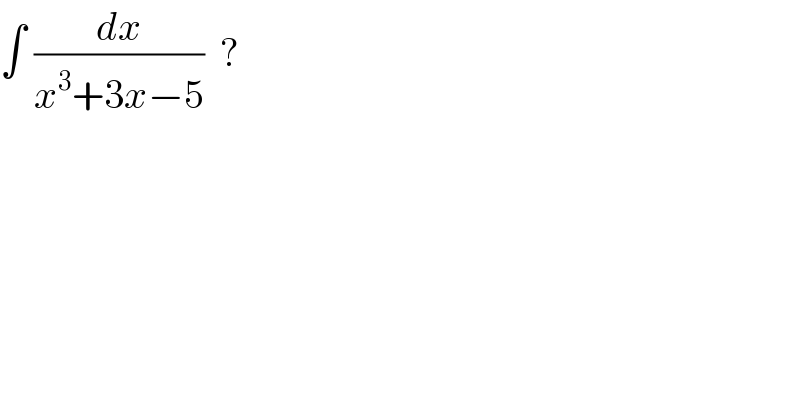
∫ (dx/(x^3 +3x−5)) ?
$$\int\:\frac{{dx}}{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{5}}\:\:? \\ $$
Commented by prakash jain last updated on 11/Jul/20
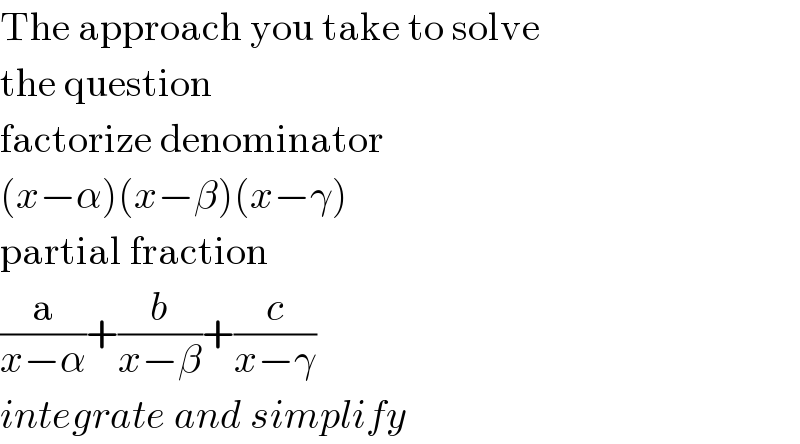
The approach you take to solve the question factorize denominator (x−α)(x−β)(x−γ) partial fraction (a/(x−α))+(b/(x−β))+(c/(x−γ)) integrate and simplify
$$\mathrm{The}\:\mathrm{approach}\:\mathrm{you}\:\mathrm{take}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{the}\:\mathrm{question} \\ $$$$\mathrm{factorize}\:\mathrm{denominator} \\ $$$$\left({x}−\alpha\right)\left({x}−\beta\right)\left({x}−\gamma\right) \\ $$$$\mathrm{partial}\:\mathrm{fraction} \\ $$$$\frac{\mathrm{a}}{{x}−\alpha}+\frac{{b}}{{x}−\beta}+\frac{{c}}{{x}−\gamma} \\ $$$${integrate}\:{and}\:{simplify} \\ $$
Answered by 1549442205 last updated on 12/Jul/20
Puttimg x=y−(1/y)⇒x^3 =y^3 −3y+(3/y)−(1/y^3 ) x^3 +3x−5=0⇔y^3 −3y+(3/y)−(1/y^3 )+3y−(3/y)−5=0 ⇔y^3 −(1/y^3 )−5=0⇔y^6 −5y^3 −1=0.This a quadratic eqs for y^3 .Δ=29 y^3 =((5±(√(29)))/2)⇔y= { ((y_1 =^3 (√((5+(√(29)))/2)))),((y_2 =^3 (√((5−(√(29)))/2)))) :} x=^3 (√((5+(√(29)))/2))−(1/(^3 (√((5+(√(29)))/2)))) =^3 (√((5+(√(29)))/2))+^3 (√((5−(√(29)))/2)) is unique root.Hence x^3 +3x−5=(x−x_0 )(x^2 +ax+b) ⇔x^3 +3x−5=x^3 +(a−x_0 )x^2 +(b−ax_0 )x+bx_0 ⇔ { ((bx_0 =−5)),((b−ax_0 =3)),((a−x_0 =0)) :} Hence, a=x_0 =^3 (√((5+(√(29)))/2))+^3 (√((5−(√(29)))/2)) ≈1.15(1) b=((−5)/(^3 (√((5+(√(29)))/2))+^3 (√((5−(√(29)))/2))))≈−4.33 (2) we find A,B,C so that (1/(x^3 +3x−5))=(A/(x−x_0 ))+((Bx+C)/(x^2 +ax+b)) ⇔(A+B)x^2 +(Aa−Bx_0 +C)x+Ab−Cx_0 =1 { ((A+B=0)),((Aa−Bx_0 +C=0)),((Ab−Cx_0 =1)) :} ⇔ { ((A(a+x_0 )+C=0)),((Ab−Cx_0 =1)) :} ⇒Ab+A(a+x_0 )=1⇒A=(1/(a+b+x_0 )) B=((−1)/(a+b+x_0 )),C=((b/(a+b+x_0 ))−1)/x_0 C=((−a−x_0 )/((a+b+x_0 )x_0 )) F=∫(dx/(x^3 +3x−5))=∫(A/(x−x_0 ))dx+∫((Bx+C)/(x^2 +ax+b))dx =Aln∣x−x_0 ∣+(B/2)∫((2x+a)/(x^2 +ax+b))dx+∫((C−((aB)/2))/(x^2 +ax+b))dx =Aln∣x−x_0 ∣+(B/2)ln∣x^2 +ax+b∣+(C−((aB)/2))∫(dx/((x+(a/2))^2 −((a^2 /4)−b))) =Aln∣x−x_0 ∣+(B/2)ln∣x^2 +ax+b∣+(C−((aB)/2))×(2/( (√(a^2 −4b))))ln∣((x+(a/2)−((√(a^2 −4b))/2))/(x+(a/2)+((√(a^2 −4b))/2)))∣
$$\mathrm{Puttimg}\:\mathrm{x}=\mathrm{y}−\frac{\mathrm{1}}{\mathrm{y}}\Rightarrow\mathrm{x}^{\mathrm{3}} =\mathrm{y}^{\mathrm{3}} −\mathrm{3y}+\frac{\mathrm{3}}{\mathrm{y}}−\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{3}} } \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{5}=\mathrm{0}\Leftrightarrow\mathrm{y}^{\mathrm{3}} −\mathrm{3y}+\frac{\mathrm{3}}{\mathrm{y}}−\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{3}} }+\mathrm{3y}−\frac{\mathrm{3}}{\mathrm{y}}−\mathrm{5}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{y}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{3}} }−\mathrm{5}=\mathrm{0}\Leftrightarrow\mathrm{y}^{\mathrm{6}} −\mathrm{5y}^{\mathrm{3}} −\mathrm{1}=\mathrm{0}.\mathrm{This} \\ $$$$\mathrm{a}\:\mathrm{quadratic}\:\mathrm{eqs}\:\mathrm{for}\:\mathrm{y}^{\mathrm{3}} .\Delta=\mathrm{29} \\ $$$$\mathrm{y}^{\mathrm{3}} =\frac{\mathrm{5}\pm\sqrt{\mathrm{29}}}{\mathrm{2}}\Leftrightarrow\mathrm{y}=\begin{cases}{\mathrm{y}_{\mathrm{1}} =\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{29}}}{\mathrm{2}}}}\\{\mathrm{y}_{\mathrm{2}} =\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{29}}}{\mathrm{2}}}}\end{cases} \\ $$$$\mathrm{x}=\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{29}}}{\mathrm{2}}}−\frac{\mathrm{1}}{\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{29}}}{\mathrm{2}}}} \\ $$$$=\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{29}}}{\mathrm{2}}}+^{\mathrm{3}} \sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{29}}}{\mathrm{2}}}\:\mathrm{is}\:\mathrm{unique} \\ $$$$\mathrm{root}.\mathrm{Hence}\:\mathrm{x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{5}=\left(\mathrm{x}−\mathrm{x}_{\mathrm{0}} \right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}\right) \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{5}=\mathrm{x}^{\mathrm{3}} +\left(\mathrm{a}−\mathrm{x}_{\mathrm{0}} \right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{b}−\mathrm{ax}_{\mathrm{0}} \right)\mathrm{x}+\mathrm{bx}_{\mathrm{0}} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{bx}_{\mathrm{0}} =−\mathrm{5}}\\{\mathrm{b}−\mathrm{ax}_{\mathrm{0}} =\mathrm{3}}\\{\mathrm{a}−\mathrm{x}_{\mathrm{0}} =\mathrm{0}}\end{cases} \\ $$$$\mathrm{Hence},\:\mathrm{a}=\mathrm{x}_{\mathrm{0}} =\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{29}}}{\mathrm{2}}}+\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{29}}}{\mathrm{2}}}\:\approx\mathrm{1}.\mathrm{15}\left(\mathrm{1}\right) \\ $$$$\mathrm{b}=\frac{−\mathrm{5}}{\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{29}}}{\mathrm{2}}}+\:^{\mathrm{3}} \sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{29}}}{\mathrm{2}}}}\approx−\mathrm{4}.\mathrm{33}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{we}\:\mathrm{find}\:\mathrm{A},\mathrm{B},\mathrm{C}\:\mathrm{so}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{5}}=\frac{\mathrm{A}}{\mathrm{x}−\mathrm{x}_{\mathrm{0}} }+\frac{\mathrm{Bx}+\mathrm{C}}{\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}} \\ $$$$\Leftrightarrow\left(\mathrm{A}+\mathrm{B}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{Aa}−\mathrm{Bx}_{\mathrm{0}} +\mathrm{C}\right)\mathrm{x}+\mathrm{Ab}−\mathrm{Cx}_{\mathrm{0}} =\mathrm{1} \\ $$$$\begin{cases}{\mathrm{A}+\mathrm{B}=\mathrm{0}}\\{\mathrm{Aa}−\mathrm{Bx}_{\mathrm{0}} +\mathrm{C}=\mathrm{0}}\\{\mathrm{Ab}−\mathrm{Cx}_{\mathrm{0}} =\mathrm{1}}\end{cases}\:\Leftrightarrow\begin{cases}{\mathrm{A}\left(\mathrm{a}+\mathrm{x}_{\mathrm{0}} \right)+\mathrm{C}=\mathrm{0}}\\{\mathrm{Ab}−\mathrm{Cx}_{\mathrm{0}} =\mathrm{1}}\end{cases} \\ $$$$\Rightarrow\mathrm{Ab}+\mathrm{A}\left(\mathrm{a}+\mathrm{x}_{\mathrm{0}} \right)=\mathrm{1}\Rightarrow\mathrm{A}=\frac{\mathrm{1}}{\mathrm{a}+\mathrm{b}+\mathrm{x}_{\mathrm{0}} } \\ $$$$\mathrm{B}=\frac{−\mathrm{1}}{\mathrm{a}+\mathrm{b}+\mathrm{x}_{\mathrm{0}} },\mathrm{C}=\left(\frac{\mathrm{b}}{\mathrm{a}+\mathrm{b}+\mathrm{x}_{\mathrm{0}} }−\mathrm{1}\right)/\mathrm{x}_{\mathrm{0}} \\ $$$$\mathrm{C}=\frac{−\mathrm{a}−\mathrm{x}_{\mathrm{0}} }{\left(\mathrm{a}+\mathrm{b}+\mathrm{x}_{\mathrm{0}} \right)\mathrm{x}_{\mathrm{0}} } \\ $$$$\mathrm{F}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{5}}=\int\frac{\mathrm{A}}{\mathrm{x}−\mathrm{x}_{\mathrm{0}} }\mathrm{dx}+\int\frac{\mathrm{Bx}+\mathrm{C}}{\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}}\mathrm{dx} \\ $$$$=\mathrm{Aln}\mid\mathrm{x}−\mathrm{x}_{\mathrm{0}} \mid+\frac{\mathrm{B}}{\mathrm{2}}\int\frac{\mathrm{2x}+\mathrm{a}}{\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}}\mathrm{dx}+\int\frac{\mathrm{C}−\frac{\mathrm{aB}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}}\mathrm{dx} \\ $$$$=\mathrm{Aln}\mid\mathrm{x}−\mathrm{x}_{\mathrm{0}} \mid+\frac{\mathrm{B}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}\mid+\left(\mathrm{C}−\frac{\mathrm{aB}}{\mathrm{2}}\right)\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{b}\right)} \\ $$$$=\mathrm{A}\boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{x}}_{\mathrm{0}} \mid+\frac{\boldsymbol{\mathrm{B}}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{ax}}+\boldsymbol{\mathrm{b}}\mid+\left(\boldsymbol{\mathrm{C}}−\frac{\boldsymbol{\mathrm{aB}}}{\mathrm{2}}\right)×\frac{\mathrm{2}}{\:\sqrt{\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{b}}}}\boldsymbol{\mathrm{ln}}\mid\frac{\boldsymbol{\mathrm{x}}+\frac{\boldsymbol{\mathrm{a}}}{\mathrm{2}}−\frac{\sqrt{\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{b}}}}{\mathrm{2}}}{\boldsymbol{\mathrm{x}}+\frac{\boldsymbol{\mathrm{a}}}{\mathrm{2}}+\frac{\sqrt{\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{b}}}}{\mathrm{2}}}\mid \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *