Menu Close

dx-x-3-x-2-x-1-

Tinku Tara 0 Comments
Pin




Question Number 121300 by liberty last updated on 06/Nov/20
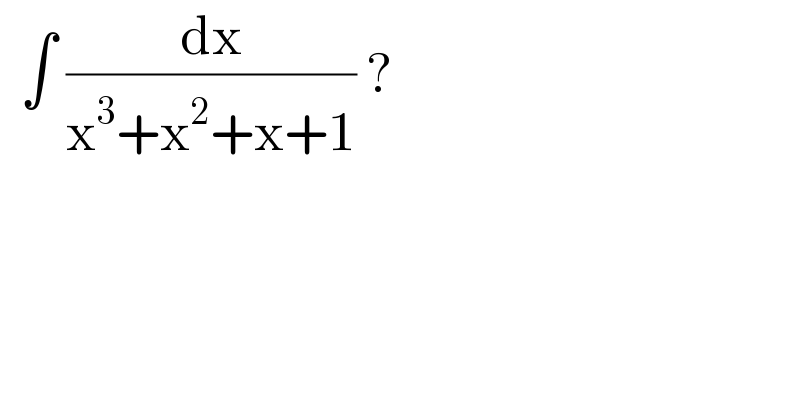
∫ (dx/(x^3 +x^2 +x+1)) ?
$$\:\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\:? \\ $$
Commented by liberty last updated on 06/Nov/20
Answered by TANMAY PANACEA last updated on 06/Nov/20
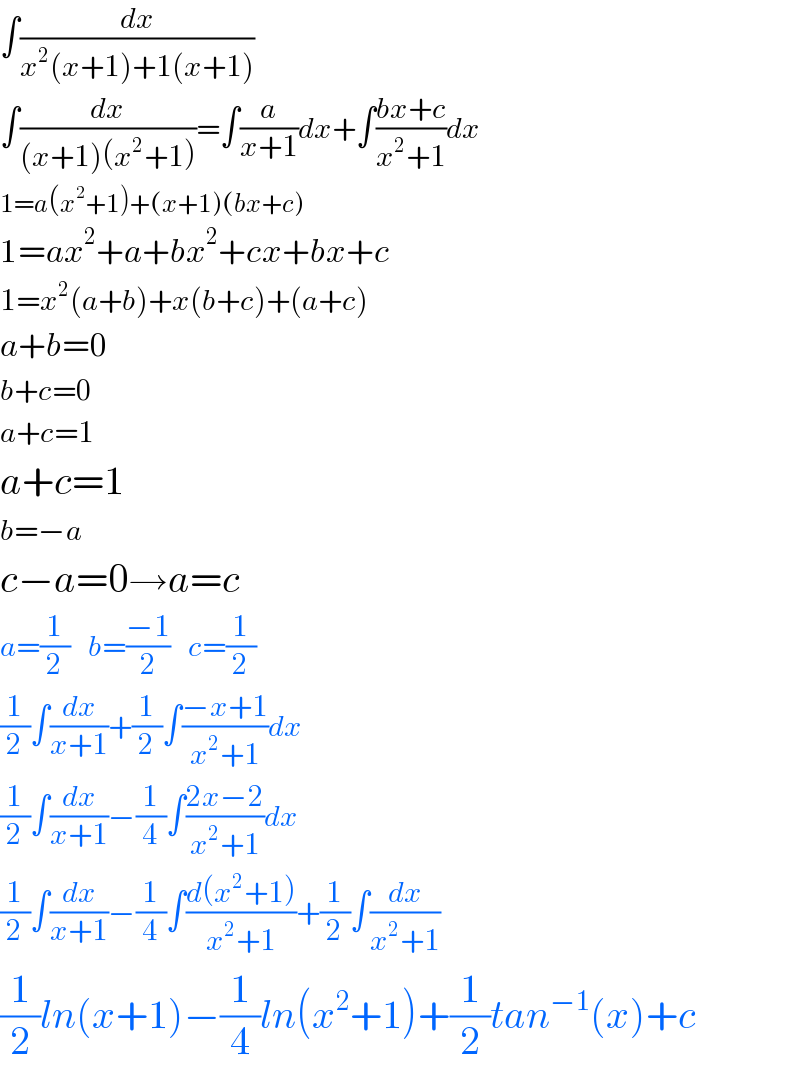
∫(dx/(x^2 (x+1)+1(x+1))) ∫(dx/((x+1)(x^2 +1)))=∫(a/(x+1))dx+∫((bx+c)/(x^2 +1))dx 1=a(x^2 +1)+(x+1)(bx+c) 1=ax^2 +a+bx^2 +cx+bx+c 1=x^2 (a+b)+x(b+c)+(a+c) a+b=0 b+c=0 a+c=1 a+c=1 b=−a c−a=0→a=c a=(1/2) b=((−1)/2) c=(1/2) (1/2)∫(dx/(x+1))+(1/2)∫((−x+1)/(x^2 +1))dx (1/2)∫(dx/(x+1))−(1/4)∫((2x−2)/(x^2 +1))dx (1/2)∫(dx/(x+1))−(1/4)∫((d(x^2 +1))/(x^2 +1))+(1/2)∫(dx/(x^2 +1)) (1/2)ln(x+1)−(1/4)ln(x^2 +1)+(1/2)tan^(−1) (x)+c
$$\int\frac{{dx}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)+\mathrm{1}\left({x}+\mathrm{1}\right)} \\ $$$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}=\int\frac{{a}}{{x}+\mathrm{1}}{dx}+\int\frac{{bx}+{c}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\mathrm{1}={a}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\left({x}+\mathrm{1}\right)\left({bx}+{c}\right) \\ $$$$\mathrm{1}={ax}^{\mathrm{2}} +{a}+{bx}^{\mathrm{2}} +{cx}+{bx}+{c} \\ $$$$\mathrm{1}={x}^{\mathrm{2}} \left({a}+{b}\right)+{x}\left({b}+{c}\right)+\left({a}+{c}\right) \\ $$$${a}+{b}=\mathrm{0} \\ $$$${b}+{c}=\mathrm{0} \\ $$$${a}+{c}=\mathrm{1} \\ $$$${a}+{c}=\mathrm{1} \\ $$$${b}=−{a} \\ $$$${c}−{a}=\mathrm{0}\rightarrow{a}={c} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:{b}=\frac{−\mathrm{1}}{\mathrm{2}}\:\:\:{c}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−{x}+\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{x}−\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{d}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left({x}\right)+{c} \\ $$
Answered by Bird last updated on 06/Nov/20
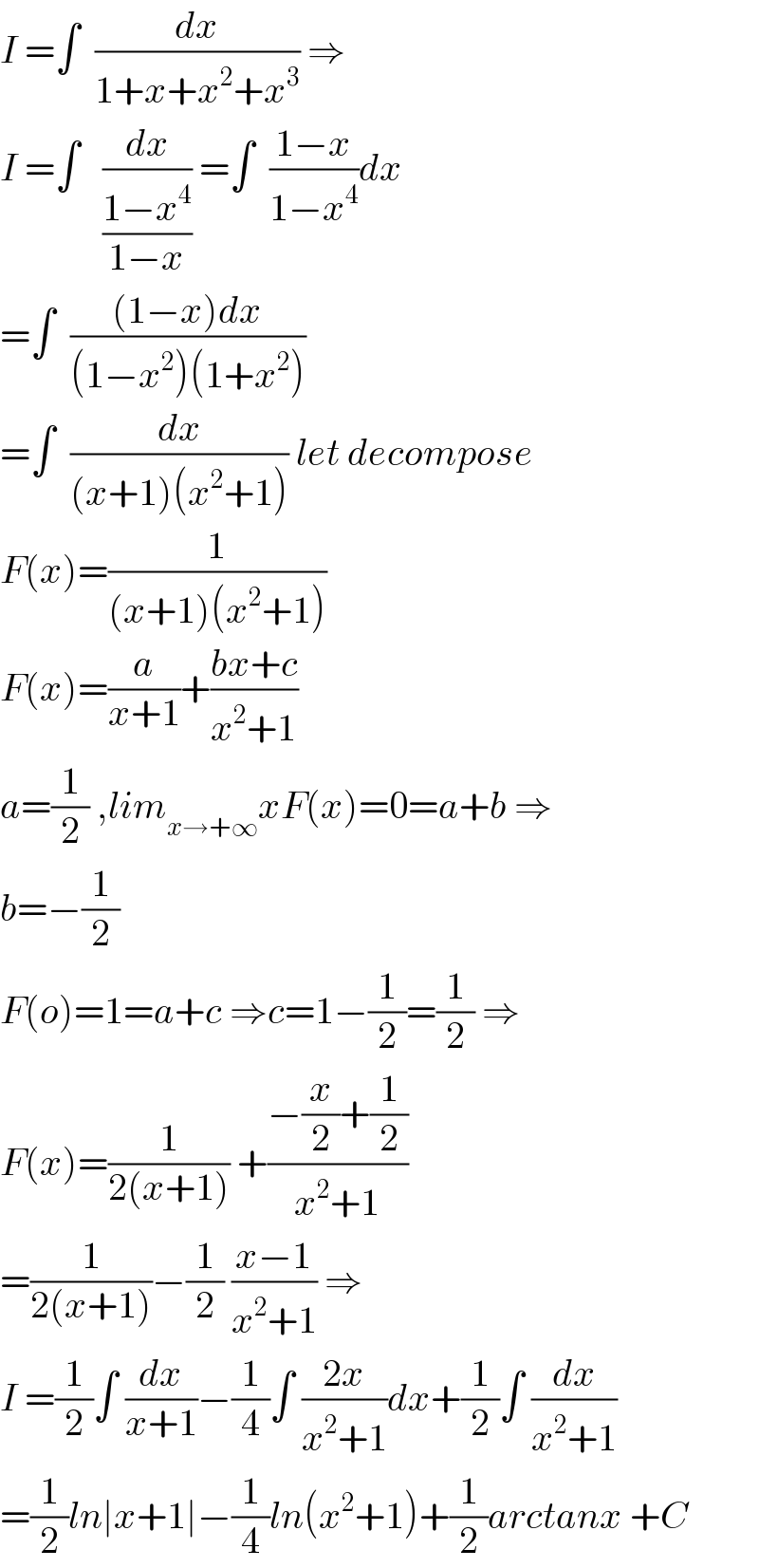
I =∫ (dx/(1+x+x^2 +x^3 )) ⇒ I =∫ (dx/((1−x^4 )/(1−x))) =∫ ((1−x)/(1−x^4 ))dx =∫ (((1−x)dx)/((1−x^2 )(1+x^2 ))) =∫ (dx/((x+1)(x^2 +1))) let decompose F(x)=(1/((x+1)(x^2 +1))) F(x)=(a/(x+1))+((bx+c)/(x^2 +1)) a=(1/2) ,lim_(x→+∞) xF(x)=0=a+b ⇒ b=−(1/2) F(o)=1=a+c ⇒c=1−(1/2)=(1/2) ⇒ F(x)=(1/(2(x+1))) +((−(x/2)+(1/2))/(x^2 +1)) =(1/(2(x+1)))−(1/2) ((x−1)/(x^2 +1)) ⇒ I =(1/2)∫ (dx/(x+1))−(1/4)∫ ((2x)/(x^2 +1))dx+(1/2)∫ (dx/(x^2 +1)) =(1/2)ln∣x+1∣−(1/4)ln(x^2 +1)+(1/2)arctanx +C
$${I}\:=\int\:\:\frac{{dx}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }\:\Rightarrow \\ $$$${I}\:=\int\:\:\:\frac{{dx}}{\frac{\mathrm{1}−{x}^{\mathrm{4}} }{\mathrm{1}−{x}}}\:=\int\:\:\frac{\mathrm{1}−{x}}{\mathrm{1}−{x}^{\mathrm{4}} }{dx} \\ $$$$=\int\:\:\frac{\left(\mathrm{1}−{x}\right){dx}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$=\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}+\mathrm{1}}+\frac{{bx}+{c}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}}\:,{lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}={a}+{b}\:\Rightarrow \\ $$$${b}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}\left({o}\right)=\mathrm{1}={a}+{c}\:\Rightarrow{c}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)}\:+\frac{−\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{arctanx}\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *