dx-x-4-1-3-

Question Number 86871 by john santu last updated on 01/Apr/20

$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Commented by mathmax by abdo last updated on 01/Apr/20

complex method I =∫ (dx/((x^4 +1)^3 )) =∫ (dx/((x^2 −i)^3 (x^2 +i)^3 )) =∫ (dx/((x−(√i))^3 (x+(√i))^3 (x−(√(−i)))^3 (x+(√(−i)))^3 )) =∫ (dx/((((x−(√i))/(x+(√i))))^3 (x+(√i))^6 (x^2 +i)^3 )) changement ((x−(√i))/(x+(√i))) =t give x−(√i)=tx+t(√i) ⇒(1−t)x =(1+t)(√i) ⇒x =((1+t)/(1−t))(√i) ⇒ (dx/dt) =((1−t+(1+t))/((1−t)^2 ))(√i)=(2/((t−1)^2 ))(√i) x+(√i)=(((1+t)/(1−t))+1)(√i)=(((1+t+1−t)/(1−t)))(√i)=(2/(1−t))(√i) and x^2 +i =((((1+t)^2 )/((1−t)^2 ))+1)i =(((t^2 +2t+1+t^2 −2t+1)/((t−1)^2 )))i =((2t^2 +2)/((t−1)^2 ))i ⇒I =∫ ((2(√i)dt)/((t−1)^2 t^3 ((2/(1−t))(√i))^6 ×8(((t^2 +1)/((t−1)^2 )))^3 )) =2(√i)∫ (((t−1)^(10) dt)/(8.2^6 t^3 ((√i))^6 (t^2 +1)^3 )) =((√i)/(4.2^6 (−i))) ∫ (((t−1)^(10) )/((t^2 +1)^3 ))dt =−(1/(4.2^6 (√i))) ∫ ((Σ_(k=0) ^(10) C_(10) ^k t^k (−1)^(10−1) )/((t^2 +1)^3 ))dt =−(1/(4.2^6 (√i)))Σ_(k=0) ^(10) (−1)^k C_(10) ^k ∫ (t^k /((t^2 +1)^3 ))dt ....be continued...

$${complex}\:{method}\:{I}\:=\int\:\:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:=\int\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{i}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} +{i}\right)^{\mathrm{3}} } \\ $$$$=\int\:\:\frac{{dx}}{\left({x}−\sqrt{{i}}\right)^{\mathrm{3}} \left({x}+\sqrt{{i}}\right)^{\mathrm{3}} \left({x}−\sqrt{−{i}}\right)^{\mathrm{3}} \left({x}+\sqrt{−{i}}\right)^{\mathrm{3}} } \\ $$$$=\int\:\:\frac{{dx}}{\left(\frac{{x}−\sqrt{{i}}}{{x}+\sqrt{{i}}}\right)^{\mathrm{3}} \left({x}+\sqrt{{i}}\right)^{\mathrm{6}} \left({x}^{\mathrm{2}} \:+{i}\right)^{\mathrm{3}} }\:{changement}\:\frac{{x}−\sqrt{{i}}}{{x}+\sqrt{{i}}}\:={t}\:{give} \\ $$$${x}−\sqrt{{i}}={tx}+{t}\sqrt{{i}}\:\Rightarrow\left(\mathrm{1}−{t}\right){x}\:=\left(\mathrm{1}+{t}\right)\sqrt{{i}}\:\Rightarrow{x}\:=\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\sqrt{{i}}\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:=\frac{\mathrm{1}−{t}+\left(\mathrm{1}+{t}\right)}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }\sqrt{{i}}=\frac{\mathrm{2}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\sqrt{{i}} \\ $$$${x}+\sqrt{{i}}=\left(\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}+\mathrm{1}\right)\sqrt{{i}}=\left(\frac{\mathrm{1}+{t}+\mathrm{1}−{t}}{\mathrm{1}−{t}}\right)\sqrt{{i}}=\frac{\mathrm{2}}{\mathrm{1}−{t}}\sqrt{{i}}\:{and} \\ $$$${x}^{\mathrm{2}} +{i}\:=\left(\frac{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }+\mathrm{1}\right){i}\:=\left(\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\right){i} \\ $$$$=\frac{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{i}\:\Rightarrow{I}\:=\int\:\:\:\:\frac{\mathrm{2}\sqrt{{i}}{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{3}} \:\left(\frac{\mathrm{2}}{\mathrm{1}−{t}}\sqrt{{i}}\right)^{\mathrm{6}} ×\mathrm{8}\left(\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\right)^{\mathrm{3}} } \\ $$$$=\mathrm{2}\sqrt{{i}}\int\:\:\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{10}} \:{dt}}{\mathrm{8}.\mathrm{2}^{\mathrm{6}} {t}^{\mathrm{3}} \left(\sqrt{{i}}\right)^{\mathrm{6}} \left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:=\frac{\sqrt{{i}}}{\mathrm{4}.\mathrm{2}^{\mathrm{6}} \left(−{i}\right)}\:\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{10}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}.\mathrm{2}^{\mathrm{6}} \sqrt{{i}}}\:\int\:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{10}} \:{C}_{\mathrm{10}} ^{{k}} \:{t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{10}−\mathrm{1}} }{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}.\mathrm{2}^{\mathrm{6}} \sqrt{{i}}}\sum_{{k}=\mathrm{0}} ^{\mathrm{10}} \left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{10}} ^{{k}} \:\int\:\:\frac{{t}^{{k}} }{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }{dt}\:….{be}\:{continued}… \\ $$$$ \\ $$

Answered by MJS last updated on 01/Apr/20

Ostrogradski ∫(dx/((x^4 +1)^3 ))= =((x(7x^4 +11))/(32(x^4 +1)^2 ))+((21)/(32))∫(dx/(x^4 +1))= we had the remaining integral lately =((x(7x^4 +11))/(32(x^4 +1)^2 ))+((21(√2))/(256))ln ((x^2 +(√2)x+1)/(x^2 −(√2)x+1)) +((21(√2))/(128))(arctan ((√2)x−1) +arctan ((√2)x+1))+C

$$\mathrm{Ostrogradski} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$=\frac{{x}\left(\mathrm{7}{x}^{\mathrm{4}} +\mathrm{11}\right)}{\mathrm{32}\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{21}}{\mathrm{32}}\int\frac{{dx}}{{x}^{\mathrm{4}} +\mathrm{1}}= \\ $$$$\mathrm{we}\:\mathrm{had}\:\mathrm{the}\:\mathrm{remaining}\:\mathrm{integral}\:\mathrm{lately} \\ $$$$=\frac{{x}\left(\mathrm{7}{x}^{\mathrm{4}} +\mathrm{11}\right)}{\mathrm{32}\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{21}\sqrt{\mathrm{2}}}{\mathrm{256}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}+\mathrm{1}}\:+\frac{\mathrm{21}\sqrt{\mathrm{2}}}{\mathrm{128}}\left(\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}−\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}+\mathrm{1}\right)\right)+{C} \\ $$

Commented by jagoll last updated on 01/Apr/20

si mjs, do you have the pdf file this method?

$$\mathrm{si}\:\mathrm{mjs},\:\mathrm{do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{the}\:\mathrm{pdf}\:\mathrm{file}\:\mathrm{this}\: \\ $$$$\mathrm{method}? \\ $$

Commented by MJS last updated on 01/Apr/20

$$\mathrm{no}\:\mathrm{but}\:\mathrm{I}\:\mathrm{can}\:\mathrm{post}\:\mathrm{it}\:\mathrm{again},\:\mathrm{wait}… \\ $$

Commented by MJS last updated on 01/Apr/20

Ostrogradski′s Method f(x)=((p(x))/(q(x))) with p(x), q(x) are polynomes and the fraction cannot be further reduced and the degree of p(x) is smaller than the degree of q(x) ∫((p(x))/(q(x)))dx=((p_1 (x))/(q_1 (x)))+∫((p_2 (x))/(q_2 (x)))dx q_1 (x)=gcf (q(x), q′(x)) q_2 (x)=((q(x))/(q_1 (x))) p_j (x) are polynomes with degree smaller than q_j (x). we find them like this: degree (q_1 )=d_1 p_1 (x)=a_0 +a_1 x+a_2 x^2 ... a_(d_1 −1) x^(d_1 −1) =Σ_(j=0) ^(d_1 −1) a_j x^j degree (q_2 )=d_2 p_2 (x)=b_0 +b_1 x+b_2 x^2 ...b_(d_2 −1) x^(d_2 −1) =Σ_(j=0) ^(d_2 −1) b_j x^j ((p(x))/(q(x)))=(d/dx)[((p_1 (x))/(q_1 (x)))]+((p_2 (x))/(q_2 (x))) by matching the constants

$$\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method} \\ $$$${f}\left({x}\right)=\frac{{p}\left({x}\right)}{{q}\left({x}\right)}\:\mathrm{with}\:{p}\left({x}\right),\:{q}\left({x}\right)\:\mathrm{are}\:\mathrm{polynomes} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{fraction}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{further}\:\mathrm{reduced} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{degree}\:\mathrm{of}\:{p}\left({x}\right)\:\mathrm{is}\:\mathrm{smaller}\:\mathrm{than}\:\mathrm{the} \\ $$$$\mathrm{degree}\:\mathrm{of}\:{q}\left({x}\right) \\ $$$$\int\frac{{p}\left({x}\right)}{{q}\left({x}\right)}{dx}=\frac{{p}_{\mathrm{1}} \left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{p}_{\mathrm{2}} \left({x}\right)}{{q}_{\mathrm{2}} \left({x}\right)}{dx} \\ $$$${q}_{\mathrm{1}} \left({x}\right)=\mathrm{gcf}\:\left({q}\left({x}\right),\:{q}'\left({x}\right)\right) \\ $$$${q}_{\mathrm{2}} \left({x}\right)=\frac{{q}\left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)} \\ $$$${p}_{{j}} \left({x}\right)\:\mathrm{are}\:\mathrm{polynomes}\:\mathrm{with}\:\mathrm{degree}\:\mathrm{smaller} \\ $$$$\mathrm{than}\:{q}_{{j}} \left({x}\right).\:\mathrm{we}\:\mathrm{find}\:\mathrm{them}\:\mathrm{like}\:\mathrm{this}: \\ $$$$\mathrm{degree}\:\left({q}_{\mathrm{1}} \right)={d}_{\mathrm{1}} \\ $$$${p}_{\mathrm{1}} \left({x}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} …\:{a}_{{d}_{\mathrm{1}} −\mathrm{1}} {x}^{{d}_{\mathrm{1}} −\mathrm{1}} =\underset{{j}=\mathrm{0}} {\overset{{d}_{\mathrm{1}} −\mathrm{1}} {\sum}}{a}_{{j}} {x}^{{j}} \\ $$$$\mathrm{degree}\:\left({q}_{\mathrm{2}} \right)={d}_{\mathrm{2}} \\ $$$${p}_{\mathrm{2}} \left({x}\right)={b}_{\mathrm{0}} +{b}_{\mathrm{1}} {x}+{b}_{\mathrm{2}} {x}^{\mathrm{2}} …{b}_{{d}_{\mathrm{2}} −\mathrm{1}} {x}^{{d}_{\mathrm{2}} −\mathrm{1}} =\underset{{j}=\mathrm{0}} {\overset{{d}_{\mathrm{2}} −\mathrm{1}} {\sum}}{b}_{{j}} {x}^{{j}} \\ $$$$\frac{{p}\left({x}\right)}{{q}\left({x}\right)}=\frac{{d}}{{dx}}\left[\frac{{p}_{\mathrm{1}} \left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)}\right]+\frac{{p}_{\mathrm{2}} \left({x}\right)}{{q}_{\mathrm{2}} \left({x}\right)} \\ $$$$\mathrm{by}\:\mathrm{matching}\:\mathrm{the}\:\mathrm{constants} \\ $$

Commented by jagoll last updated on 01/Apr/20

$$\mathrm{thank}\:\mathrm{mister}.\:\mathrm{i}\:\mathrm{can}\:\mathrm{save}\:\mathrm{your}\:\mathrm{post} \\ $$

Commented by MJS last updated on 01/Apr/20

example ∫((x^3 +1)/((x^2 +2)^3 ))dx p(x)=x^3 +1; q(x)=(x^2 +2)^3 q′(x)=6x(x^2 +2)^2 q_1 (x)=gcf ((x^2 +2)^3 , 6x(x^2 +2)^2 )=(x^2 +2)^2 q_2 (x)=(((x^2 +2)^3 )/((x^2 +2)^2 ))=x^2 +2 ((x^3 +1)/((x+2)^3 ))=(d/dx)[((a_0 +a_1 x+a_2 x^2 +a_3 x^3 )/((x^2 +2)^2 ))]+((b_0 +b_1 x)/(x^2 +2)) ((x^3 +1)/((x+2)^3 ))=(((a_1 +2a_2 x+3a_3 x^2 )(x^2 +2)^2 −(a_0 +a_1 x+a_2 x^2 +a_3 x^3 )4x(x^2 +2))/((x^2 +2)^4 ))+((b_0 +b_1 x)/(x^2 +2)) ((x^3 +1)/((x+2)^3 ))=(((a_1 +2a_2 x+3a_3 x^2 )(x^2 +2)−(a_0 +a_1 x+a_2 x^2 +a_3 x^3 )4x)/((x^2 +2)^3 ))+(((b_0 +b_1 x)(x^2 +2)^2 )/((x^2 +2)^3 )) x^3 +1=(a_1 +2a_2 x+3a_3 x^2 )(x^2 +2)−(a_0 +a_1 x+a_2 x^2 +a_3 x^3 )4x+(b_0 +b_1 x)(x^2 +2)^2 b_1 x^5 −(a_3 −b_0 )x^4 −(2a_2 −4b_1 +1)x^3 −(3a_1 −6a_3 −4b_0 )x^2 −4(a_0 −a_2 −b_1 )x+2a_1 −4b_0 −1=0 ⇒ a_0 =−(1/2), a_1 =(5/(16)), a_2 =−(1/2), a_3 =(3/(32)), b_0 =(3/(32)), b_1 =0 ⇒ p_1 (x)=(1/(32))(3x^3 −16x^2 +10x−16) p_2 (x)=(3/(32)) ⇒ ∫((x^3 +1)/((x^2 +2)^3 ))dx=((3x^3 −16x^2 +10x−16)/(32(x^2 +2)^2 ))+(3/(32))∫(dx/(x^2 +2))= =((3x^3 −16x^2 +10x−16)/(32(x^2 +2)^2 ))+((3(√2))/(64))arctan (((√2)x)/2) +C

$$\mathrm{example} \\ $$$$\int\frac{{x}^{\mathrm{3}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }{dx} \\ $$$${p}\left({x}\right)={x}^{\mathrm{3}} +\mathrm{1};\:{q}\left({x}\right)=\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} \\ $$$${q}'\left({x}\right)=\mathrm{6}{x}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} \\ $$$${q}_{\mathrm{1}} \left({x}\right)=\mathrm{gcf}\:\left(\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} ,\:\mathrm{6}{x}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} \right)=\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} \\ $$$${q}_{\mathrm{2}} \left({x}\right)=\frac{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }={x}^{\mathrm{2}} +\mathrm{2} \\ $$$$\frac{{x}^{\mathrm{3}} +\mathrm{1}}{\left({x}+\mathrm{2}\right)^{\mathrm{3}} }=\frac{{d}}{{dx}}\left[\frac{{a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{3}} {x}^{\mathrm{3}} }{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\right]+\frac{{b}_{\mathrm{0}} +{b}_{\mathrm{1}} {x}}{{x}^{\mathrm{2}} +\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{3}} +\mathrm{1}}{\left({x}+\mathrm{2}\right)^{\mathrm{3}} }=\frac{\left({a}_{\mathrm{1}} +\mathrm{2}{a}_{\mathrm{2}} {x}+\mathrm{3}{a}_{\mathrm{3}} {x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\left({a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{3}} {x}^{\mathrm{3}} \right)\mathrm{4}{x}\left({x}^{\mathrm{2}} +\mathrm{2}\right)}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{4}} }+\frac{{b}_{\mathrm{0}} +{b}_{\mathrm{1}} {x}}{{x}^{\mathrm{2}} +\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{3}} +\mathrm{1}}{\left({x}+\mathrm{2}\right)^{\mathrm{3}} }=\frac{\left({a}_{\mathrm{1}} +\mathrm{2}{a}_{\mathrm{2}} {x}+\mathrm{3}{a}_{\mathrm{3}} {x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)−\left({a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{3}} {x}^{\mathrm{3}} \right)\mathrm{4}{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }+\frac{\left({b}_{\mathrm{0}} +{b}_{\mathrm{1}} {x}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} } \\ $$$${x}^{\mathrm{3}} +\mathrm{1}=\left({a}_{\mathrm{1}} +\mathrm{2}{a}_{\mathrm{2}} {x}+\mathrm{3}{a}_{\mathrm{3}} {x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)−\left({a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{3}} {x}^{\mathrm{3}} \right)\mathrm{4}{x}+\left({b}_{\mathrm{0}} +{b}_{\mathrm{1}} {x}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} \\ $$$${b}_{\mathrm{1}} {x}^{\mathrm{5}} −\left({a}_{\mathrm{3}} −{b}_{\mathrm{0}} \right){x}^{\mathrm{4}} −\left(\mathrm{2}{a}_{\mathrm{2}} −\mathrm{4}{b}_{\mathrm{1}} +\mathrm{1}\right){x}^{\mathrm{3}} −\left(\mathrm{3}{a}_{\mathrm{1}} −\mathrm{6}{a}_{\mathrm{3}} −\mathrm{4}{b}_{\mathrm{0}} \right){x}^{\mathrm{2}} −\mathrm{4}\left({a}_{\mathrm{0}} −{a}_{\mathrm{2}} −{b}_{\mathrm{1}} \right){x}+\mathrm{2}{a}_{\mathrm{1}} −\mathrm{4}{b}_{\mathrm{0}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${a}_{\mathrm{0}} =−\frac{\mathrm{1}}{\mathrm{2}},\:{a}_{\mathrm{1}} =\frac{\mathrm{5}}{\mathrm{16}},\:{a}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}},\:{a}_{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{32}},\:{b}_{\mathrm{0}} =\frac{\mathrm{3}}{\mathrm{32}},\:{b}_{\mathrm{1}} =\mathrm{0} \\ $$$$\Rightarrow \\ $$$${p}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{3}{x}^{\mathrm{3}} −\mathrm{16}{x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{16}\right) \\ $$$${p}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{3}}{\mathrm{32}} \\ $$$$\Rightarrow \\ $$$$\int\frac{{x}^{\mathrm{3}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }{dx}=\frac{\mathrm{3}{x}^{\mathrm{3}} −\mathrm{16}{x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{16}}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{32}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}}= \\ $$$$=\frac{\mathrm{3}{x}^{\mathrm{3}} −\mathrm{16}{x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{16}}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}{x}}{\mathrm{2}}\:+{C} \\ $$

Commented by MJS last updated on 01/Apr/20

it′s not always faster, but somehow smooth...

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{always}\:\mathrm{faster},\:\mathrm{but}\:\mathrm{somehow}\:\mathrm{smooth}… \\ $$

Commented by M±th+et£s last updated on 01/Apr/20

$${god}\:{bless}\:{you}\:{sir}\: \\ $$

Commented by jagoll last updated on 01/Apr/20

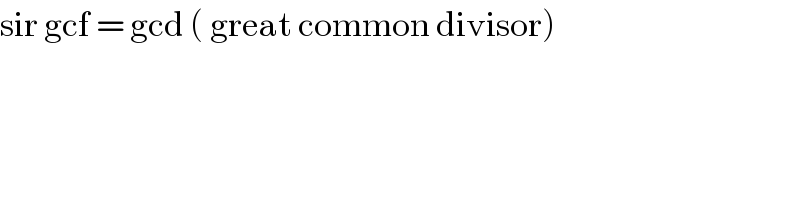
$$\mathrm{sir}\:\mathrm{gcf}\:=\:\mathrm{gcd}\:\left(\:\mathrm{great}\:\mathrm{common}\:\mathrm{divisor}\right) \\ $$

Commented by MJS last updated on 01/Apr/20

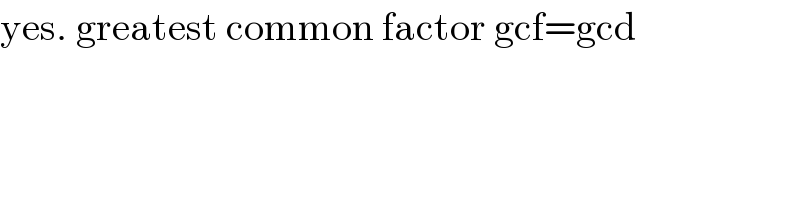
$$\mathrm{yes}.\:\mathrm{greatest}\:\mathrm{common}\:\mathrm{factor}\:\mathrm{gcf}=\mathrm{gcd} \\ $$

Answered by redmiiuser last updated on 01/Apr/20

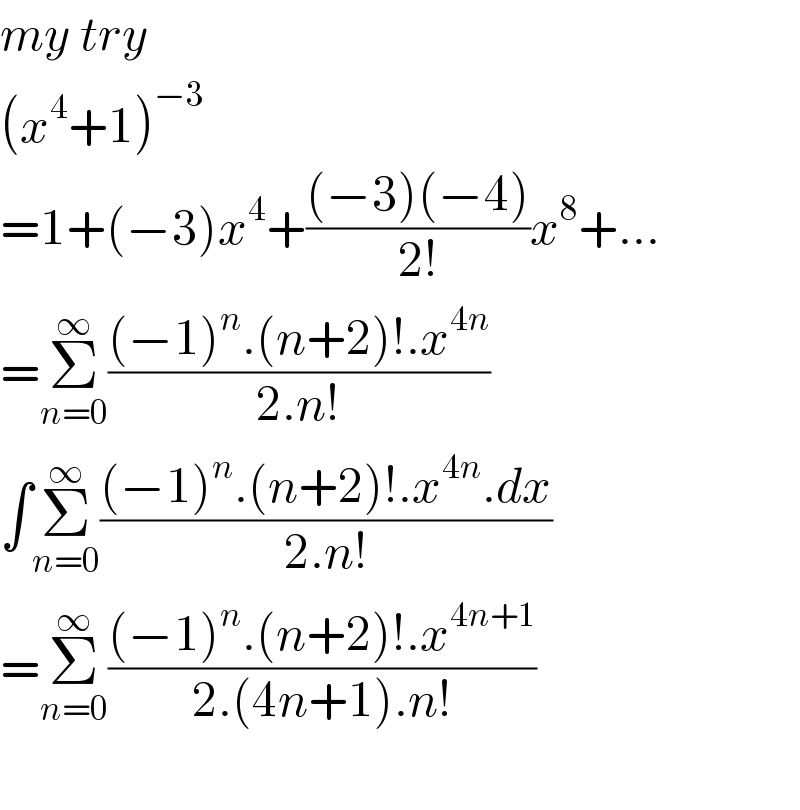
my try (x^4 +1)^(−3) =1+(−3)x^4 +(((−3)(−4))/(2!))x^8 +... =Σ_(n=0) ^∞ (((−1)^n .(n+2)!.x^(4n) )/(2.n!)) ∫Σ_(n=0) ^∞ (((−1)^n .(n+2)!.x^(4n) .dx)/(2.n!)) =Σ_(n=0) ^∞ (((−1)^n .(n+2)!.x^(4n+1) )/(2.(4n+1).n!))

$${my}\:{try} \\ $$$$\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{−\mathrm{3}} \\ $$$$=\mathrm{1}+\left(−\mathrm{3}\right){x}^{\mathrm{4}} +\frac{\left(−\mathrm{3}\right)\left(−\mathrm{4}\right)}{\mathrm{2}!}{x}^{\mathrm{8}} +… \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} .\left({n}+\mathrm{2}\right)!.{x}^{\mathrm{4}{n}} }{\mathrm{2}.{n}!} \\ $$$$\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} .\left({n}+\mathrm{2}\right)!.{x}^{\mathrm{4}{n}} .{dx}}{\mathrm{2}.{n}!} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} .\left({n}+\mathrm{2}\right)!.{x}^{\mathrm{4}{n}+\mathrm{1}} }{\mathrm{2}.\left(\mathrm{4}{n}+\mathrm{1}\right).{n}!} \\ $$$$ \\ $$

Commented by redmiiuser last updated on 01/Apr/20

$${I}\:{hope}\:{it}\:{is}\:{a}\:{smooth} \\ $$$${and}\:{efficent}\:{process} \\ $$

Commented by MJS last updated on 01/Apr/20

it′s great to solve otherwise unsolveable integrals but who wants infinit series when there′s a closed form?

$$\mathrm{it}'\mathrm{s}\:\mathrm{great}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{otherwise}\:\mathrm{unsolveable} \\ $$$$\mathrm{integrals}\:\mathrm{but}\:\mathrm{who}\:\mathrm{wants}\:\mathrm{infinit}\:\mathrm{series}\:\mathrm{when} \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{closed}\:\mathrm{form}? \\ $$

Commented by redmiiuser last updated on 01/Apr/20

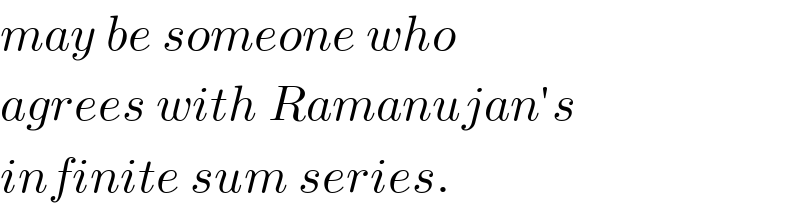
$${may}\:{be}\:{someone}\:{who} \\ $$$${agrees}\:{with}\:{Ramanujan}'{s} \\ $$$${infinite}\:{sum}\:{series}. \\ $$

Commented by MJS last updated on 01/Apr/20

it′s not a matter of agreement, it′s a matter of practicability

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{a}\:\mathrm{matter}\:\mathrm{of}\:\mathrm{agreement},\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{matter} \\ $$$$\mathrm{of}\:\mathrm{practicability} \\ $$

Commented by redmiiuser last updated on 01/Apr/20

$${thanks}\:{sir}. \\ $$

Commented by MJS last updated on 01/Apr/20

thank you for this method, I had not seen it on this forum before

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{this}\:\mathrm{method},\:\mathrm{I}\:\mathrm{had}\:\mathrm{not}\:\mathrm{seen}\:\mathrm{it} \\ $$$$\mathrm{on}\:\mathrm{this}\:\mathrm{forum}\:\mathrm{before} \\ $$

Commented by redmiiuser last updated on 01/Apr/20

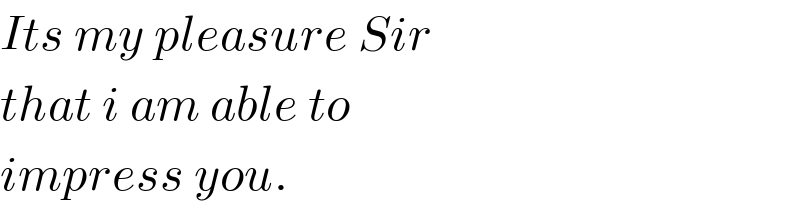
$${Its}\:{my}\:{pleasure}\:{Sir} \\ $$$${that}\:{i}\:{am}\:{able}\:{to}\: \\ $$$${impress}\:{you}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply