Question Number 114161 by bemath last updated on 17/Sep/20
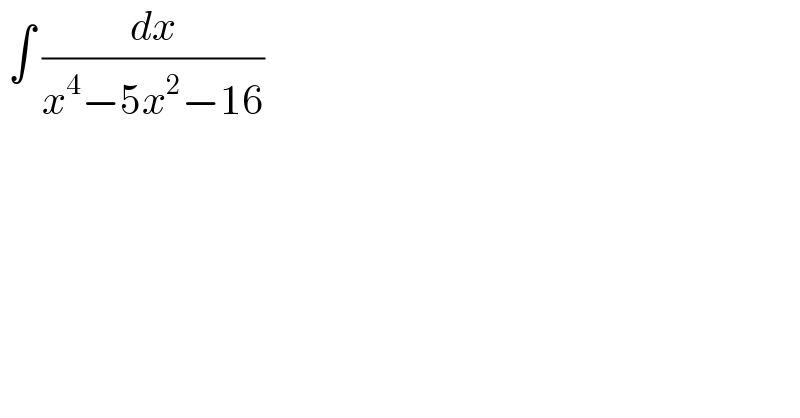
$$\:\int\:\frac{{dx}}{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} −\mathrm{16}} \\ $$
Answered by Olaf last updated on 17/Sep/20
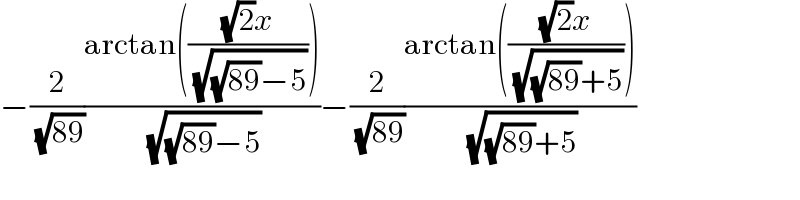
$$−\frac{\mathrm{2}}{\:\sqrt{\mathrm{89}}}\frac{\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{\sqrt{\mathrm{89}}−\mathrm{5}}}\right)}{\:\sqrt{\sqrt{\mathrm{89}}−\mathrm{5}}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{89}}}\frac{\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{\sqrt{\mathrm{89}}+\mathrm{5}}}\right)}{\:\sqrt{\sqrt{\mathrm{89}}+\mathrm{5}}} \\ $$
Answered by malwan last updated on 17/Sep/20
![∫(( dx)/([x^2 −(((5+(√(89)))/2))][x^2 −(((5−(√(89)))/2))])) =∫(( dx)/((x+(√((5+(√(89)))/2)))(x−(√((5+(√(89)))/2)))(x+(√((5−(√(89)))/2)))(x−(√((5−(√(89)))/2))))) =∫(( dx)/((x+a)(x−a)(x+b)(x−b))) =(1/(2a(a+b)(−a+b))) ln∣ x+a ∣ + (1/(2a(a+b)(a−b))) ln∣ x−a ∣ + (1/(2b(a+b)(a−b))) ln ∣ x+b ∣ + (1/(2b(−a+b)(a+b))) ln∣ x−b ∣ =(1/(2a(b^2 −a^2 ))) ln ∣x+a ∣ + (1/(2a(a^2 −b^2 ))) ln ∣x−a ∣ + (1/(2b(a^2 −b^2 ))) ln ∣ x+b ∣ + (1/(2b(b^2 −a^2 ))) ln ∣ x−b ∣ now a=(√((5+(√(89)))/2)) ; b=(√((5−(√(89)))/2)) a^2 −b^2 = (√(89)) ; b^2 −a^2 = −(√(89))](https://www.tinkutara.com/question/Q114205.png)
$$\int\frac{\:{dx}}{\left[{x}^{\mathrm{2}} −\left(\frac{\mathrm{5}+\sqrt{\mathrm{89}}}{\mathrm{2}}\right)\right]\left[{x}^{\mathrm{2}} −\left(\frac{\mathrm{5}−\sqrt{\mathrm{89}}}{\mathrm{2}}\right)\right]} \\ $$$$=\int\frac{\:{dx}}{\left({x}+\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{89}}}{\mathrm{2}}}\right)\left({x}−\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{89}}}{\mathrm{2}}}\right)\left({x}+\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{89}}}{\mathrm{2}}}\right)\left({x}−\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{89}}}{\mathrm{2}}}\right)} \\ $$$$=\int\frac{\:{dx}}{\left({x}+{a}\right)\left({x}−{a}\right)\left({x}+{b}\right)\left({x}−{b}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}\left({a}+{b}\right)\left(−{a}+{b}\right)}\:{ln}\mid\:{x}+{a}\:\mid\:+ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}\left({a}+{b}\right)\left({a}−{b}\right)}\:{ln}\mid\:{x}−{a}\:\mid\:+ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{b}\left({a}+{b}\right)\left({a}−{b}\right)}\:{ln}\:\mid\:{x}+{b}\:\mid\:+ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{b}\left(−{a}+{b}\right)\left({a}+{b}\right)}\:{ln}\mid\:{x}−{b}\:\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}\:{ln}\:\mid{x}+{a}\:\mid\:+ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\:{ln}\:\mid{x}−{a}\:\mid\:+ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{b}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\:{ln}\:\mid\:{x}+{b}\:\mid\:+ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{b}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}\:{ln}\:\mid\:{x}−{b}\:\mid \\ $$$${now}\:{a}=\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{89}}}{\mathrm{2}}}\:;\:{b}=\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{89}}}{\mathrm{2}}} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\:\sqrt{\mathrm{89}}\:;\:{b}^{\mathrm{2}} −{a}^{\mathrm{2}} =\:−\sqrt{\mathrm{89}} \\ $$
