Menu Close

dx-x-4-x-2-1-

Tinku Tara 0 Comments
Pin




Question Number 118010 by TANMAY PANACEA last updated on 14/Oct/20
∫(dx/(x^4 +x^2 +1))
$$\int\frac{{dx}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by mmmmmm1 last updated on 14/Oct/20
(d/dx)[((f(x))/(g(x)))]= ((g(x)∙(d/dx)[f(x)] − f(x)∙(d/dx)[g(x)])/(g(x)^2 )) ((d−3x^4 d−x^2 d)/((x^4 +x^2 +1)^2 ))
$$\:\:\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\left[\frac{\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)}\right]=\:\frac{\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)\centerdot\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\left[\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\right]\:−\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\centerdot\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\left[\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)\right]}{\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)^{\mathrm{2}} } \\ $$$$\:\:\frac{\boldsymbol{{d}}−\mathrm{3}\boldsymbol{{x}}^{\mathrm{4}} \boldsymbol{{d}}−\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{d}}}{\left(\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by MJS_new last updated on 14/Oct/20
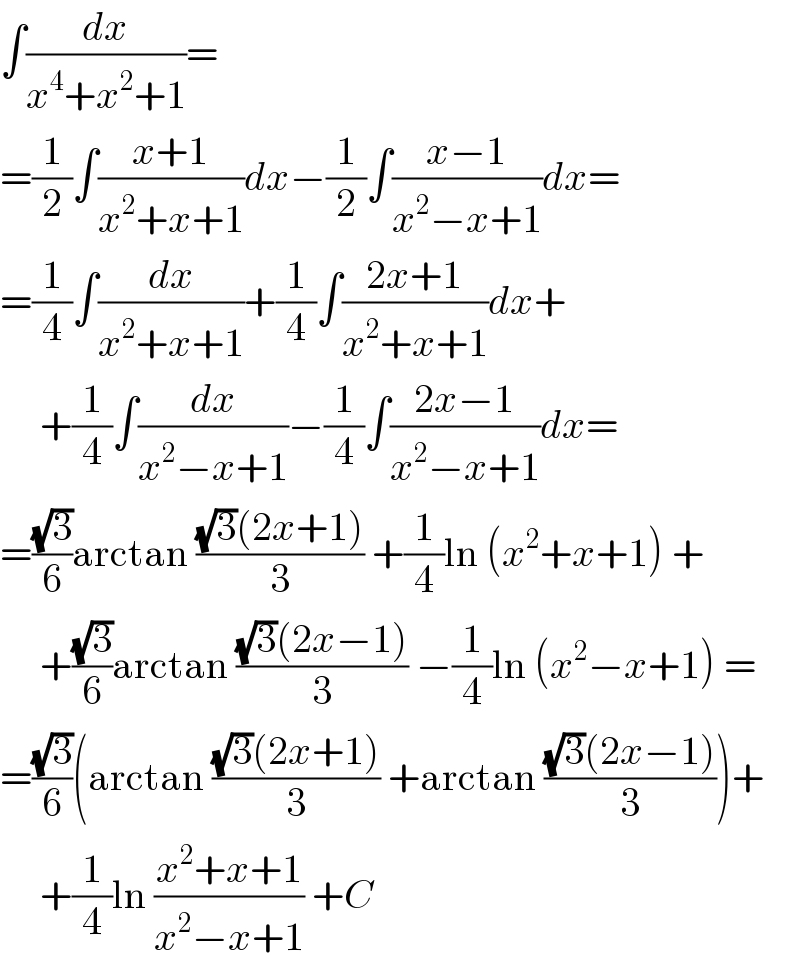
∫(dx/(x^4 +x^2 +1))= =(1/2)∫((x+1)/(x^2 +x+1))dx−(1/2)∫((x−1)/(x^2 −x+1))dx= =(1/4)∫(dx/(x^2 +x+1))+(1/4)∫((2x+1)/(x^2 +x+1))dx+ +(1/4)∫(dx/(x^2 −x+1))−(1/4)∫((2x−1)/(x^2 −x+1))dx= =((√3)/6)arctan (((√3)(2x+1))/3) +(1/4)ln (x^2 +x+1) + +((√3)/6)arctan (((√3)(2x−1))/3) −(1/4)ln (x^2 −x+1) = =((√3)/6)(arctan (((√3)(2x+1))/3) +arctan (((√3)(2x−1))/3))+ +(1/4)ln ((x^2 +x+1)/(x^2 −x+1)) +C
$$\int\frac{{dx}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}+ \\ $$$$\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\:+ \\ $$$$\:\:\:\:\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\left(\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\right)+ \\ $$$$\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:+{C} \\ $$
Answered by TANMAY PANACEA last updated on 14/Oct/20
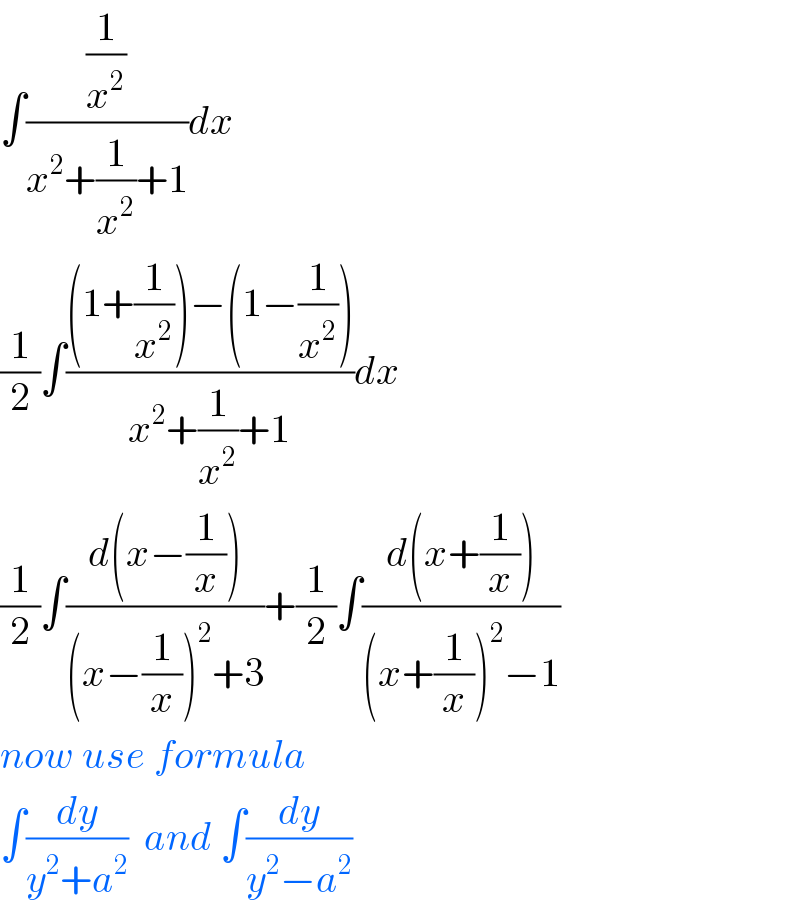
∫((1/x^2 )/(x^2 +(1/x^2 )+1))dx (1/2)∫(((1+(1/x^2 ))−(1−(1/x^2 )))/(x^2 +(1/x^2 )+1))dx (1/2)∫((d(x−(1/x)))/((x−(1/x))^2 +3))+(1/2)∫((d(x+(1/x)))/((x+(1/x))^2 −1)) now use formula ∫(dy/(y^2 +a^2 )) and ∫(dy/(y^2 −a^2 ))
$$\int\frac{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$${now}\:{use}\:{formula} \\ $$$$\int\frac{{dy}}{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:\:{and}\:\int\frac{{dy}}{{y}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 14/Oct/20
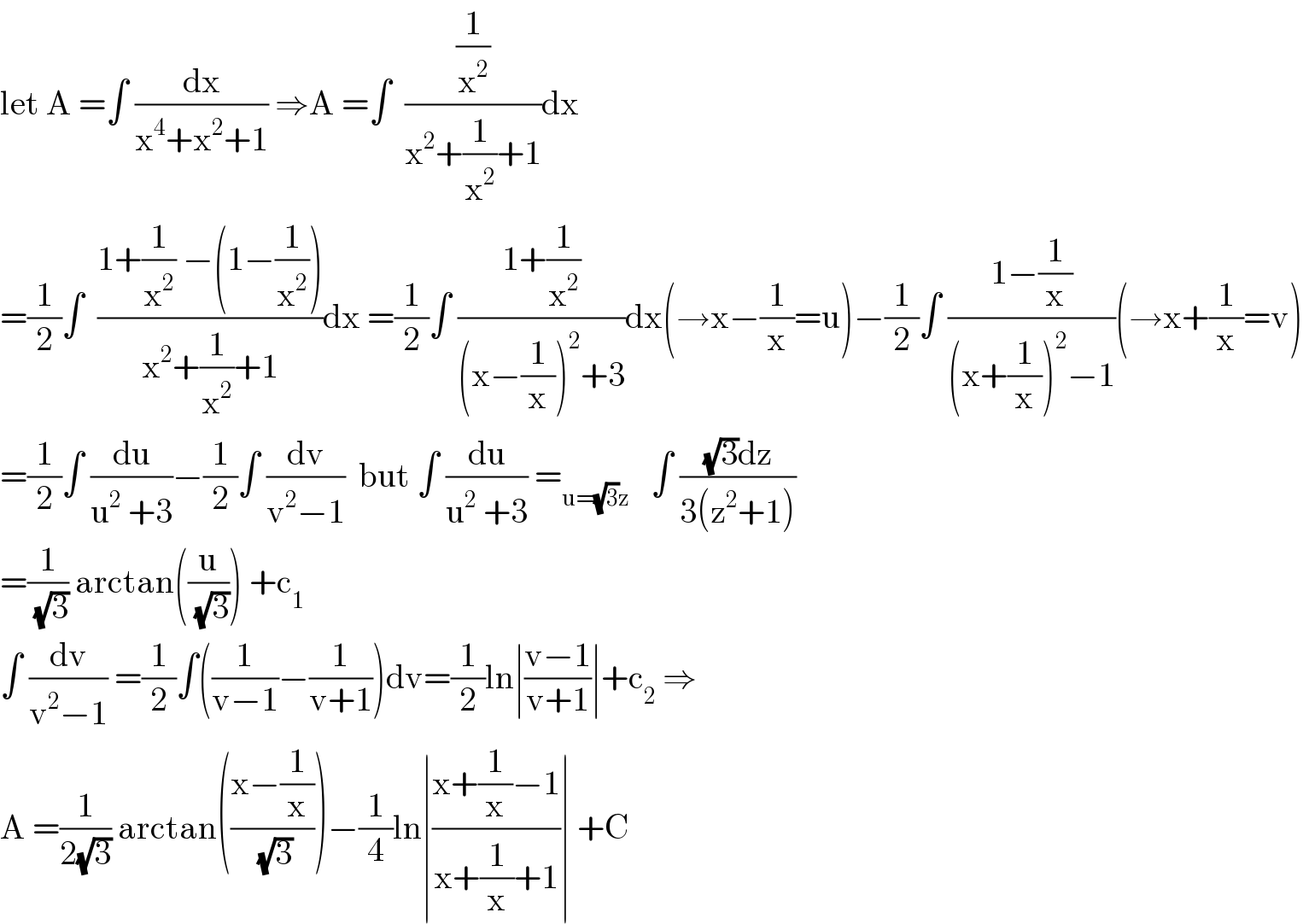
let A =∫ (dx/(x^4 +x^2 +1)) ⇒A =∫ ((1/x^2 )/(x^2 +(1/x^2 )+1))dx =(1/2)∫ ((1+(1/x^2 ) −(1−(1/x^2 )))/(x^2 +(1/x^2 )+1))dx =(1/2)∫ ((1+(1/x^2 ))/((x−(1/x))^2 +3))dx(→x−(1/x)=u)−(1/2)∫ ((1−(1/x))/((x+(1/x))^2 −1))(→x+(1/x)=v) =(1/2)∫ (du/(u^2 +3))−(1/2)∫ (dv/(v^2 −1)) but ∫ (du/(u^2 +3)) =_(u=(√3)z) ∫ (((√3)dz)/(3(z^2 +1))) =(1/( (√3))) arctan((u/( (√3)))) +c_1 ∫ (dv/(v^2 −1)) =(1/2)∫((1/(v−1))−(1/(v+1)))dv=(1/2)ln∣((v−1)/(v+1))∣+c_2 ⇒ A =(1/(2(√3))) arctan(((x−(1/x))/( (√3))))−(1/4)ln∣((x+(1/x)−1)/(x+(1/x)+1))∣ +C
$$\mathrm{let}\:\mathrm{A}\:=\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow\mathrm{A}\:=\int\:\:\frac{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{3}}\mathrm{dx}\left(\rightarrow\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{u}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{1}}\left(\rightarrow\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{v}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{1}}\:\:\mathrm{but}\:\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{3}}\:=_{\mathrm{u}=\sqrt{\mathrm{3}}\mathrm{z}} \:\:\:\int\:\frac{\sqrt{\mathrm{3}}\mathrm{dz}}{\mathrm{3}\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{u}}{\:\sqrt{\mathrm{3}}}\right)\:+\mathrm{c}_{\mathrm{1}} \\ $$$$\int\:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{v}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{v}+\mathrm{1}}\right)\mathrm{dv}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{v}−\mathrm{1}}{\mathrm{v}+\mathrm{1}}\mid+\mathrm{c}_{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}}{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{1}}\mid\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *