Menu Close

dx-x-4-x-2-a-2-

Tinku Tara 0 Comments
Pin




Question Number 146147 by iloveisrael last updated on 11/Jul/21
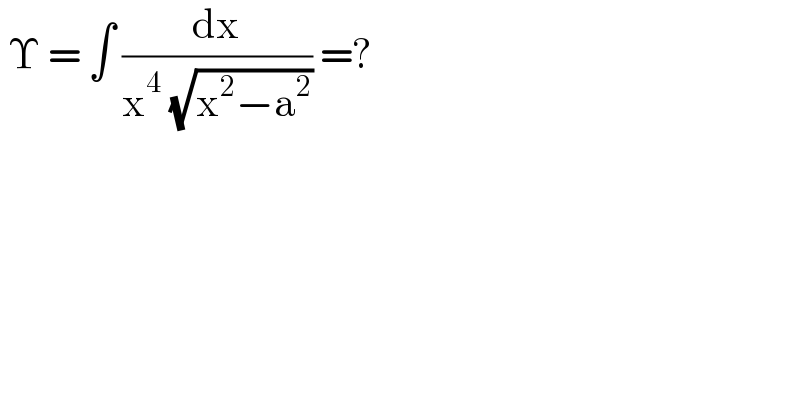
Υ = ∫ (dx/(x^4 (√(x^2 −a^2 )))) =?
$$\:\Upsilon\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}\:=? \\ $$
Answered by EDWIN88 last updated on 11/Jul/21
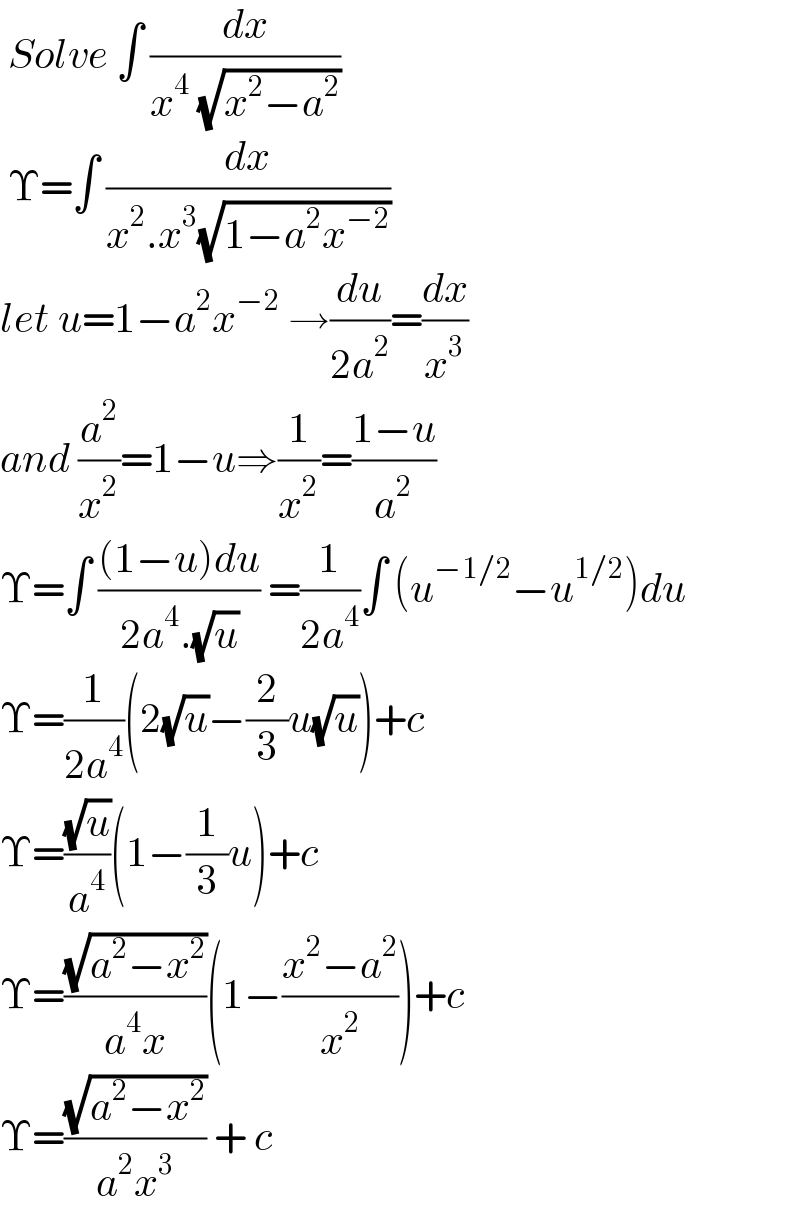
Solve ∫ (dx/(x^4 (√(x^2 −a^2 )))) Υ=∫ (dx/(x^2 .x^3 (√(1−a^2 x^(−2) )))) let u=1−a^2 x^(−2) →(du/(2a^2 ))=(dx/x^3 ) and (a^2 /x^2 )=1−u⇒(1/x^2 )=((1−u)/a^2 ) Υ=∫ (((1−u)du)/(2a^4 .(√u))) =(1/(2a^4 ))∫ (u^(−1/2) −u^(1/2) )du Υ=(1/(2a^4 ))(2(√u)−(2/3)u(√u))+c Υ=((√u)/a^4 )(1−(1/3)u)+c Υ=((√(a^2 −x^2 ))/(a^4 x))(1−((x^2 −a^2 )/x^2 ))+c Υ=((√(a^2 −x^2 ))/(a^2 x^3 )) + c
$$\:{Solve}\:\int\:\frac{{dx}}{{x}^{\mathrm{4}} \:\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}\: \\ $$$$\:\Upsilon=\int\:\frac{{dx}}{{x}^{\mathrm{2}} .{x}^{\mathrm{3}} \sqrt{\mathrm{1}−{a}^{\mathrm{2}} {x}^{−\mathrm{2}} }}\: \\ $$$${let}\:{u}=\mathrm{1}−{a}^{\mathrm{2}} {x}^{−\mathrm{2}} \:\rightarrow\frac{{du}}{\mathrm{2}{a}^{\mathrm{2}} }=\frac{{dx}}{{x}^{\mathrm{3}} } \\ $$$${and}\:\frac{{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }=\mathrm{1}−{u}\Rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\frac{\mathrm{1}−{u}}{{a}^{\mathrm{2}} } \\ $$$$\Upsilon=\int\:\frac{\left(\mathrm{1}−{u}\right){du}}{\mathrm{2}{a}^{\mathrm{4}} .\sqrt{{u}}}\:=\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{4}} }\int\:\left({u}^{−\mathrm{1}/\mathrm{2}} −{u}^{\mathrm{1}/\mathrm{2}} \right){du} \\ $$$$\Upsilon=\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{4}} }\left(\mathrm{2}\sqrt{{u}}−\frac{\mathrm{2}}{\mathrm{3}}{u}\sqrt{{u}}\right)+{c}\: \\ $$$$\Upsilon=\frac{\sqrt{{u}}}{{a}^{\mathrm{4}} }\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}{u}\right)+{c}\: \\ $$$$\Upsilon=\frac{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{{a}^{\mathrm{4}} {x}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)+{c} \\ $$$$\Upsilon=\frac{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{{a}^{\mathrm{2}} {x}^{\mathrm{3}} }\:+\:{c}\:\: \\ $$
Answered by mathmax by abdo last updated on 11/Jul/21
Υ=_(x=(a/(sint))) ∫ ((sin^4 t)/(a^4 (√((a^2 /(sin^2 t))−a^2 ))))(−((acost)/(sin^2 t)))dt =(1/a^4 )∫ ((sin^2 t .cost)/(cost))sint dt =(1/a^4 )∫ sin^3 t dt sin^3 t =sint(((1−cos(2t))/2))=(1/2)(sint−sint cos(2t)) sint cos(2t)=cos((π/2)−t)cos(2t)=(1/2){cos((π/2)+t)+cos((π/2)−3t)) =(1/2){−sint+sin(3t)} ⇒sin^3 t=(1/2)sint−(1/4){−sint+sin(3t)} =(3/4)sint−(1/4)sin(3t) ⇒Υ=(1/a^4 )∫ ((3/4)sint−(1/4)sin(3t))dt =−(3/(4a^4 ))cost +(1/(12a^4 ))cos(3t) +K sint=(a/x) ⇒cost =(√(1−(a^2 /x^2 ))) cos(3t)=cost .cos2t−sint sin(2t) =cost(2cos^2 t−1)−2sin^2 t cost =(√(1−(a^2 /x^2 )))(2(1−(a^2 /x^2 ))−1)−2(a^2 /x^2 )(√(1−(a^2 /x^2 ))) ⇒ Ψ=−(3/(4a^4 ))(√(1−(a^2 /x^2 )))+(1/(12a^4 ))(√(1−(a^2 /x^2 )))(1−((4a^2 )/x^2 )) +K
$$\Upsilon=_{\mathrm{x}=\frac{\mathrm{a}}{\mathrm{sint}}} \:\:\:\int\:\:\frac{\mathrm{sin}^{\mathrm{4}} \mathrm{t}}{\mathrm{a}^{\mathrm{4}} \sqrt{\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}−\mathrm{a}^{\mathrm{2}} }}\left(−\frac{\mathrm{acost}}{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{4}} }\int\:\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:.\mathrm{cost}}{\mathrm{cost}}\mathrm{sint}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{4}} }\int\:\mathrm{sin}^{\mathrm{3}} \mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{sin}^{\mathrm{3}} \mathrm{t}\:=\mathrm{sint}\left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sint}−\mathrm{sint}\:\mathrm{cos}\left(\mathrm{2t}\right)\right) \\ $$$$\mathrm{sint}\:\mathrm{cos}\left(\mathrm{2t}\right)=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{t}\right)\mathrm{cos}\left(\mathrm{2t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}+\mathrm{t}\right)+\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{3t}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\mathrm{sint}+\mathrm{sin}\left(\mathrm{3t}\right)\right\}\:\Rightarrow\mathrm{sin}^{\mathrm{3}} \mathrm{t}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sint}−\frac{\mathrm{1}}{\mathrm{4}}\left\{−\mathrm{sint}+\mathrm{sin}\left(\mathrm{3t}\right)\right\} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sint}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{3t}\right)\:\Rightarrow\Upsilon=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{4}} }\int\:\left(\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sint}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{3t}\right)\right)\mathrm{dt} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{4a}^{\mathrm{4}} }\mathrm{cost}\:+\frac{\mathrm{1}}{\mathrm{12a}^{\mathrm{4}} }\mathrm{cos}\left(\mathrm{3t}\right)\:+\mathrm{K} \\ $$$$\mathrm{sint}=\frac{\mathrm{a}}{\mathrm{x}}\:\Rightarrow\mathrm{cost}\:=\sqrt{\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\left(\mathrm{3t}\right)=\mathrm{cost}\:.\mathrm{cos2t}−\mathrm{sint}\:\mathrm{sin}\left(\mathrm{2t}\right) \\ $$$$=\mathrm{cost}\left(\mathrm{2cos}^{\mathrm{2}} \mathrm{t}−\mathrm{1}\right)−\mathrm{2sin}^{\mathrm{2}} \mathrm{t}\:\mathrm{cost} \\ $$$$=\sqrt{\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}\left(\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\right)−\mathrm{1}\right)−\mathrm{2}\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\sqrt{\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\Psi=−\frac{\mathrm{3}}{\mathrm{4a}^{\mathrm{4}} }\sqrt{\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\mathrm{12a}^{\mathrm{4}} }\sqrt{\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }}\left(\mathrm{1}−\frac{\mathrm{4a}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\right)\:+\mathrm{K} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *