Question Number 116418 by bemath last updated on 03/Oct/20
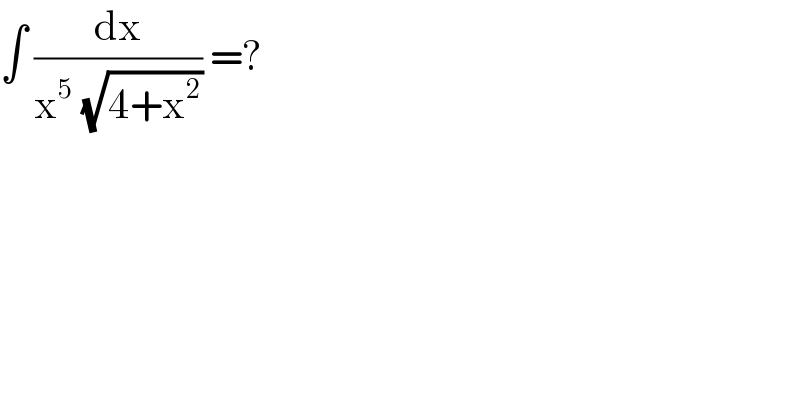
$$\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{5}} \:\sqrt{\mathrm{4}+\mathrm{x}^{\mathrm{2}} }}\:=? \\ $$
Answered by MJS_new last updated on 03/Oct/20
![∫(dx/(x^5 (√(4+x^2 ))))= [x=t−(1/t) ⇔ t=((x+(√(4+x^2 )))/2) → dx=((2(√(4+x^2 )))/(x+(√(4+x^2 ))))dt] =∫(t^4 /((t^2 −1)^5 ))dt= [Ostrogeadski′s Method] =((t(t^2 +1)(3t^4 −14t^2 +3))/(128(t^2 −1)^4 ))+(3/(128))∫(dt/(t^2 −1))= =((t(t^2 +1)(3t^4 −14t^2 +3))/(128(t^2 −1)^4 ))+(3/(256))ln ((t−1)/(t+1)) = =(((3x^2 −8)(√(4+x^2 )))/(128x^4 ))+(3/(256))ln ((−2+(√(4+x^2 )))/x) +C](https://www.tinkutara.com/question/Q116422.png)
$$\int\frac{{dx}}{{x}^{\mathrm{5}} \sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:\left[{x}={t}−\frac{\mathrm{1}}{{t}}\:\Leftrightarrow\:{t}=\frac{{x}+\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{{x}+\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{dt}\right] \\ $$$$=\int\frac{{t}^{\mathrm{4}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{5}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogeadski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}{t}^{\mathrm{4}} −\mathrm{14}{t}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{128}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{3}}{\mathrm{128}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}= \\ $$$$=\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}{t}^{\mathrm{4}} −\mathrm{14}{t}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{128}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{3}}{\mathrm{256}}\mathrm{ln}\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\:= \\ $$$$=\frac{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{8}\right)\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{\mathrm{128}{x}^{\mathrm{4}} }+\frac{\mathrm{3}}{\mathrm{256}}\mathrm{ln}\:\frac{−\mathrm{2}+\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{{x}}\:+{C} \\ $$
Answered by MJS_new last updated on 04/Oct/20
![easier: ∫(dx/(x^5 (√(4+x^2 ))))= [t=(√(4+x^2 )) → dx=((√(4+x^2 ))/x)] =∫(dt/((t^2 −4)^3 ))= [Ostrogradski again] =((t(3t^2 −20))/(128(t^2 −4)^2 ))+(3/(128))∫(dt/(t^2 −4))= =((t(3t^2 −20))/(128(t^2 −4)^2 ))+(3/(512))ln ((t−2)/(t+2)) = =(((3x^2 −8)(√(4+x^2 )))/(128x^4 ))+(3/(256))ln ((−2+(√(4+x^2 )))/x) +C](https://www.tinkutara.com/question/Q116423.png)
$$\mathrm{easier}: \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{5}} \sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{{x}}\right] \\ $$$$=\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{3}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\:\mathrm{again}\right] \\ $$$$=\frac{{t}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{20}\right)}{\mathrm{128}\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{128}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{4}}= \\ $$$$=\frac{{t}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{20}\right)}{\mathrm{128}\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{512}}\mathrm{ln}\:\frac{{t}−\mathrm{2}}{{t}+\mathrm{2}}\:= \\ $$$$=\frac{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{8}\right)\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{\mathrm{128}{x}^{\mathrm{4}} }+\frac{\mathrm{3}}{\mathrm{256}}\mathrm{ln}\:\frac{−\mathrm{2}+\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}{{x}}\:+{C} \\ $$
